C++ Math: Exercises, Practice, Solution

C++ Math [35 exercises with solution]

[An editor is available at the bottom of the page to write and execute the scripts. Go to the editor]

1. Write a C++ program to check whether a given number is a power of two or not.
Is 8 is power of 2: True
Is 256 is power of 2: True
Is 124 is power of 2: False
Click me to see the sample solution

2. Write a C++ program to check the additive persistence of a given number.
Additive Persistence
Consider the process of taking a number, adding its digits, then adding the digits of the number derived from it, etc., until the remaining number has only one digit. The number of additions required to obtain a single digit from a number n is called the additive persistence of n, and the digit obtained is called the digital root of n.
For example, the sequence obtained from the starting number 9876 is (9876, 30, 3), so 9876 has an additive persistence of 2 and a digital root of 3. The additive persistences of the first few positive integers are 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, ... (OEIS A031286). The smallest numbers of additive persistence n for n=0, 1, ... are 0, 10, 19, 199, 19999999999999999999999, ... (OEIS A006050).
Source: https://mathworld.wolfram.com/
Click me to see the sample solution

3. Write a C++ program to reverse the digits of a given integer.
Sample Input: 4
Sample Output: 4

Sample Input: 123
Sample Output: 321
Click me to see the sample solution

4. Write a C++ program to divide two integers (dividend and divisor) without using the multiplication, division and mod operators.
Dividend 7 Divisor 2
Result: 3
Dividend -17 Divisor 5
Result: -3
Click me to see the sample solution

5. Write a C++ program to calculate x raised to the power n (xⁿ).
Sample Input: x = 7.0
n = 2
Sample Output: 49
Click me to see the sample solution

6. Write a C++ program to get the fraction part from two given integers representing the numerator and denominator in string format.
Sample Input: x = 3
n = 2
Sample Output: 1.5
Click me to see the sample solution

7. Write a C++ program to get the Excel column title that corresponds to a given column number (integer value).
For example:
1 -> A
2 -> B
3 -> C
...
26 -> Z
27 -> AA
28 -> AB
...
Click me to see the sample solution

8. Write a C++ program to get the column number (integer value) that corresponds to a column title as it appears on an Excel sheet.
For example:
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
Click me to see the sample solution

9. Write a C++ program to find the number of trailing zeroes in a given factorial.
Sample Input: n = 4
Sample Output: 0
Sample Input: n = 6
Sample Output: 1
Click me to see the sample solution

10. Write a C++ program to count the total number of digits 1 appearing in all positive integers less than or equal to a given integer n.
Example:
Sample Input: n = 12,
Sample Output: 5
Return 5, because digit 1 occurred 5 times in the following numbers: 1, 10, 11, 12.
Click me to see the sample solution

11. Write a C++ program to add repeatedly all digits of a given non-negative number until the result has only one digit.
Example:
Sample Input: 58
Sample Output: 4
Explanation: The formula is like: 5 + 8 = 13, 1 + 3 = 4.
Click me to see the sample solution

12. Write a C++ program to check if a given integer is a power of three or not.
Sample Input: 9
Sample Output: true
Sample Input: 15
Sample Output: False
Click me to see the sample solution

13. For a non negative integer in the range 0 = i = n write a C++ program to calculate the number of 1's in their binary representation and return them as an array.
Original number: 4
0 1 1 2 1
Original number: 7
0 1 1 2 1 2 2 3
Click me to see the sample solution

14. Write a C++ program to get the maximum product of a given integer after breaking the integer into the sum of at least two positive integers.
Sample Input: 12
Sample Output: 81
Explanation: 12 = 3 + 3 + 3 + 3, 3 x 3 x 3 x 3 = 81.
Sample Input: 7
Sample Output: 12
Explanation: 7 = 3 + 2 + 2, 3 x 2 x 2 = 12.
Click me to see the sample solution

15. Write a C++ program to find the nth digit of the number 1 to n?
Infinite integer sequence: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 .. where n is a positive integer.
Input: 7
Output: 7
Input: 12
Output: 1
The 12th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is 1, which is part of the number 11.
Click me to see the sample solution

16. Write a C++ program to find the square root of a number using the Babylonian method.
Sample Input: n = 50
Sample Output: 7.07107
Sample Input: n = 81
Sample Output: 9
Click me to see the sample solution

17. Write a C++ program to multiply two integers without using multiplication, division, bitwise operators, and loops.
Sample Input: 8, 9
Sample Output: 72

Input: -11, 19
Output: -209
Click me to see the sample solution

18. Write a C++ program to convert a given integer to a Roman numeral.
From Wikipedia:
Roman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers in this system are represented by combinations of letters from the Latin alphabet. Modern usage employs seven symbols, each with a fixed integer value:[1]

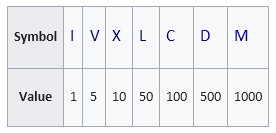
Sample Input: n = 7
Sample Output: Roman VII

Input: n = 19
Output: Roman XIX
Click me to see the sample solution

19. Write a C++ program to convert a given integer to a Roman numeral.
Sample Input: n = VII
Sample Output: Integer 7

Input: n = XIX
Output: Integer 19
Click me to see the sample solution

20. Write a C++ program to calculate the product of two positive integers represented as strings. Return the result as a string.
Sample Input: sn1 = "12"
sn2 = "5"
Sample Output: 12 X 5 = 60

Sample Input: sn1 = "48"
sn2 = "85"
Sample Output: 48 X 85 = 4080
Click me to see the sample solution

21. A decimal number is defined as a number whose whole number and fractional parts are separated by a decimal point in algebra. Write a C++ program to check if a given string is a decimal number or not.
List of characters of a valid decimal number:
Numbers: 0-9
Positive/negative sign - "+"/"-"
Decimal point - "."
Exponent - "e"
Sample Input: s = 9
Sample Output: Is 0 a decimal number? 1

Input: s = abc 123
Output: Is abc 123 a decimal number? 0
Click me to see the sample solution

22. Write a C++ program to compute the sum of a pair of binary strings. Binary strings will be returned, and input strings shouldn't be blank or contain just 1 or 0 characters.
Sample Input: bstr1 = "10"
bstr2 = "1"
Sample Output: 10 + 1 = 11

Sample Input: bstr1 = "1100"
bstr2 = "1010"
Sample Output: 1100 + 1010 = 10110
Click me to see the sample solution

23. Write a C++ program to compute the square root of a given non-negative integer. Return type should be an integer.
Sample Input: n = 81
Sample Output: Square root of 81 = 9
Input: n = 8
Output: Square root of 8 = 2
Click me to see the sample solution

24. Write a C++ program to count prime numbers less than a given positive number.
Sample Input: n = 8
Sample Output: Number of prime numbers less than 8 is 2
Sample Input: n = 30
Sample Output: Number of prime numbers less than 30 is 10
Click me to see the sample solution

25. Write a C++ program to count the total number of digits 1 present in all positive numbers less than or equal to a given integer.
Sample Input: n = 10
Sample Output: Number of digit 1 present in all +ve numbers less than or equal to 10 is 2
Sample Input: n = 19
Sample Output: Number of digit 1 present in all +ve numbers less than or equal to 19 is 12
Click me to see the sample solution

26. Write a C++ program to find the missing number in a given array of integers taken from the sequence 0, 1, 2, 3, ...,n.
Sample Input: arr[10] = {10, 9, 4, 6, 3, 2, 5, 7, 1, 0 }
Sample Output: Missing number in the said array: 8
Sample Input: arr1[4] = {0, 3, 4, 2}
Sample Output: Missing number in the said array: 1
Click me to see the sample solution

27. Write a C++ program to find the number of perfect squares (e.g. 1, 4, 9, 16, ...) that represent the sum of a given number.
Sample Input: n = 5
Number of perfect square whose sum equal to 5 = 2
Sample Input: n = 7
Number of perfect square whose sum equal to 7 = 4
Click me to see the sample solution

28. Write a C++ program to break a given integer into at least two parts (positive integers) to maximize the product of those integers.
Sample Input: n = 5
After breaking in +ve integers maximumn product from 5 = 6
Sample Input: n = 12
After breaking in +ve integers maximumn product from 12 = 81
Click me to see the sample solution

29. Write a C++ program that takes a number (n) and counts all numbers with distinct digits of length y within a specified range.
Range: 0 <= y < 10ⁿ
Test Data:
1) -> 10
(2) -> 91
Click me to see the sample solution

30. Write a C++ program to check whether a given positive integer is a perfect square or not.
In mathematics, a square number or perfect square is an integer that is the square of an integer, in other words, it is the product of some integer with itself. For example, 9 is a square number, since it can be written as 3 x 3.
Sample Input: n = 1
Is 1 is perfect number? 1
Sample Input: n = 13
Is 13 is perfect number? 0
Click me to see the sample solution

31. Write a C++ program to replace a given number until it becomes 1. If the given number(n) is even replace n with n/2 and if the number(n) is odd replace n with either n+1 or n-1. Find the minimum number of replacements.
If the given number(n) is even replace n with n/2 and if the given number(n) is odd replace n with either n+1 or n-1. Find the minimum number of replacements.
Sample Input: n = 8
Number of replacements: 3
Sample Input: n = 10
Number of replacements: 4
Click me to see the sample solution

32. Write a C++ program to find the number of arithmetic slices in a given array of integers.
From Wikipedia
In mathematics, an arithmetic progression (AP) or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant. Difference here means the second minus the first. For instance, the sequence 5, 7, 9, 11, 13, 15, . . . is an arithmetic progression with common difference of 2.
Test Data:
Original array: 1 2 3 9 4 5 6
Number of arithmetic slices: 2
Original array: 1 3 5 7
Number of arithmetic slices: 3
Original array: 2 1 3 4 7
Number of arithmetic slices: 0
Click me to see the sample solution

33. Write a C++ program to count from 1 to a specified number and display each number as the product of its prime factors.
Test Data:
Display each number as the product of its prime factors:
From 1 to 23-
1: 1
2: 2
3: 3
4: 2 x 2
5: 5
6: 2 x 3
7: 7
8: 2 x 2 x 2
9: 3 x 3
10: 2 x 5
11: 11
12: 2 x 2 x 3
13: 13
14: 2 x 7
15: 3 x 5
16: 2 x 2 x 2 x 2
17: 17
18: 2 x 3 x 3
19: 19
20: 2 x 2 x 5
21: 3 x 7
22: 2 x 11
23: 23
Click me to see the sample solution

34. Write a function which returns an array or collection which contains the prime decomposition of a given number greater than 1.
By the fundamental theorem of arithmetic, every positive integer has a unique prime factorization. Given a general algorithm for integer factorization, any integer can be factored into its constituent prime factors by repeated application of this algorithm.
The prime decomposition of a number consists of a list of prime numbers which, when multiplied together, equal the number.
Test Data:

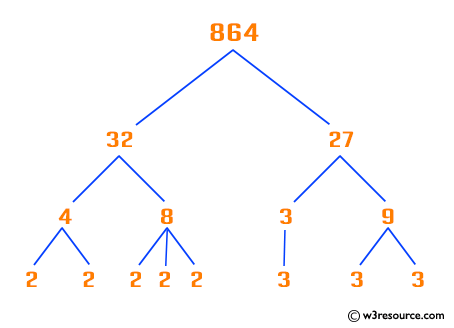
Click me to see the sample solution

35. Write a C++ program to generate a sequence of primes by means of trial division.
Trial division is the most laborious but easiest to understand of the integer factorization algorithms. The essential idea behind trial division tests to see if an integer n, the integer to be factored, can be divided by each number in turn that is less than n. For example, for the integer n = 12, the only numbers that divide it are 1, 2, 3, 4, 6, 12. Selecting only the largest powers of primes in this list gives that 12 = 3 x 4 = 3 x 2².
Test Data:
Prime numbers upto 200:
[ 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 ]
Found 46 primes
Click me to see the sample solution

CPP Code Editor:

More to Come !

Do not submit any solution of the above exercises at here, if you want to contribute go to the appropriate exercise page.