C++ Exercises: Prime decomposition

Last update on April 12 2025 12:58:23 (UTC/GMT +8 hours)

34. Prime Decomposition of a Given Number

Write a function which returns an array or collection which contains the prime decomposition of a given number greater than 1.

By the fundamental theorem of arithmetic, every positive integer has a unique prime factorization. Given a general algorithm for integer factorization, any integer can be factored into its constituent prime factors by repeated application of this algorithm.
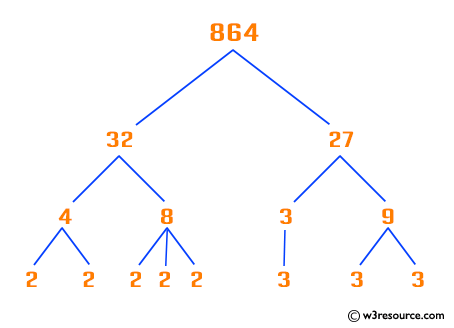
The prime decomposition of a number consists of a list of prime numbers which, when multiplied together, equal the number.

Example: 18 = 2 x 3 x 3
So prime decomposition of 18 is {2, 3, 3}

Test Data:

Sample Solution:

C++ Code :

#include <iostream>
#include <vector>

// Alias declarations for better readability
using long_pair = std::pair<long, long>; // Alias for a pair of long values
using lp_vec = std::vector<long_pair>;   // Alias for a vector of long_pair
using namespace std;

// Function to factorize a number and return its prime decomposition
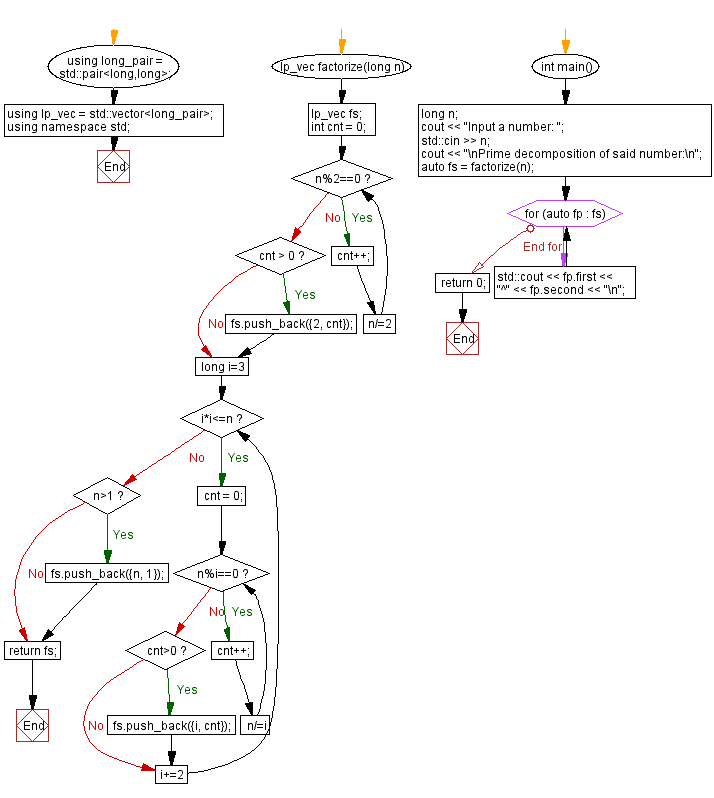
lp_vec factorize(long n) {
    lp_vec fs; // Create a vector of pairs to store factors and their counts
    int cnt = 0; // Initialize a counter for factor exponentiation

    // Factorize using 2, since 2 is the only even prime number
    for (; n % 2 == 0; n /= 2) 
        cnt++; // Increment counter for the power of 2
    if (cnt > 0)
        fs.push_back({2, cnt}); // Store factor and its count in the vector

    // Continue factorizing using odd numbers starting from 3
    for (long i = 3; i * i <= n; i += 2) {
        cnt = 0; // Reset counter for the new factor
        for (; n % i == 0; n /= i) 
            cnt++; // Increment counter for the power of the factor 'i'
        if (cnt > 0)
            fs.push_back({i, cnt}); // Store factor and its count in the vector
    }

    // If there is a remaining factor greater than 1, add it to the vector
    if (n > 1)
        fs.push_back({n, 1});

    return fs; // Return the vector with prime decomposition
}

int main() {
    long n;
    cout << "Input a number: ";
    cin >> n; // Take user input for the number to factorize

    cout << "\nPrime decomposition of the given number:\n";
    auto fs = factorize(n); // Calculate prime factors and their counts

    // Display each factor and its power in the prime decomposition
    for (auto fp : fs) {
        cout << fp.first << "^" << fp.second << "\n";
    }

    return 0;
}

Sample Output:

Input a number: 18
Prime decomposition of said number:
2^1
3^2

Flowchart:

For more Practice: Solve these Related Problems:

• Write a C++ program to perform prime factorization of an integer using recursion and return the factors in a vector.
• Write a C++ program that decomposes a number into its prime factors and prints them in ascending order.
• Write a C++ program to implement a function that returns an array containing the prime factors of a given number, including multiplicities.
• Write a C++ program to factorize a number into primes using trial division and display the result in exponent form.

C++ Code Editor:

Click to Open Editor

Contribute your code and comments through Disqus.

Previous: Number as the multiplication of its prime factors.