C++ Exercises: Generate sequence of primes by means of trial division

C++ Math: Exercise-35 with Solution

Write a C++ program to generate a sequence of primes by means of trial division.

Trial division is the most laborious but easiest to understand of the integer factorization algorithms. The essential idea behind trial division tests to see if an integer n, the integer to be factored, can be divided by each number in turn that is less than n. For example, for the integer n = 12, the only numbers that divide it are 1, 2, 3, 4, 6, 12. Selecting only the largest powers of primes in this list gives that 12 = 3 x 4 = 3 x 2².

Example: 18 = 2 x 3 x 3
So prime decomposition of 18 is {2, 3, 3}

Test Data:
[ 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 ]
Found 46 primes.

Sample Solution:

C++ Code :

#include <math.h>
#include <iostream>
#include <iomanip>

// Function to check if a number is prime
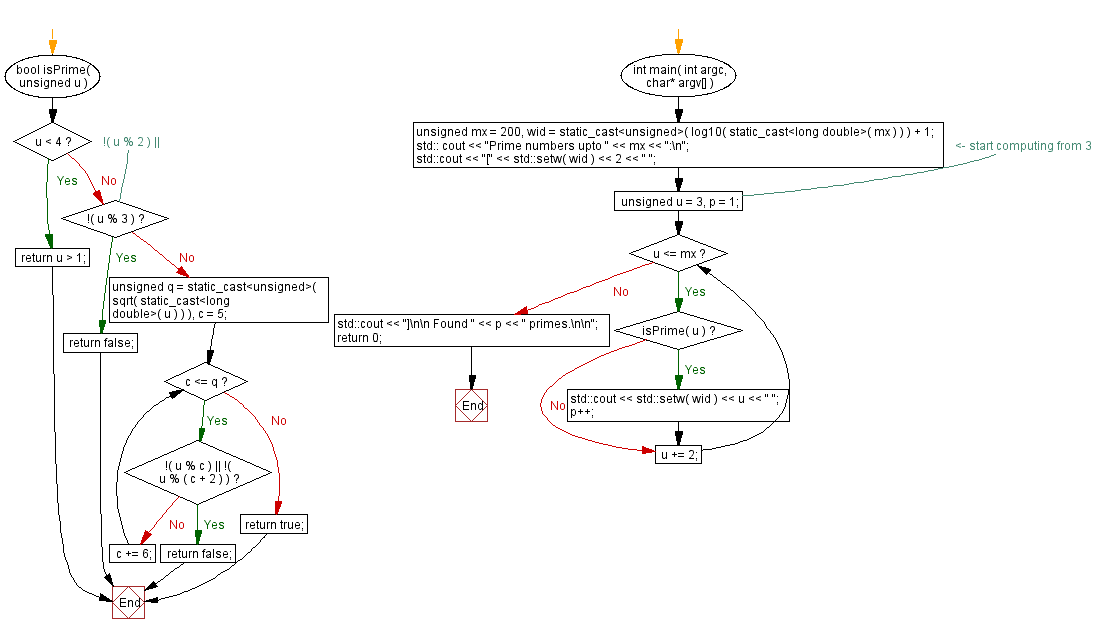
bool isPrime(unsigned u) {
    if (u < 4) return u > 1; // Numbers less than 4 are prime if greater than 1
    if (!(u % 3)) return false; // If divisible by 3, it's not prime

    // Determine potential divisors
    unsigned q = static_cast<unsigned>(sqrt(static_cast<long double>(u)));
    unsigned c = 5; // Starting divisor
    while (c <= q) {
        // Check for divisibility by c and (c+2) to optimize prime checking
        if (!(u % c) || !(u % (c + 2))) return false;
        c += 6; // Increment c by 6 (skipping multiples of 2 and 3)
    }
    return true; // If not divisible, the number is prime
}

int main(int argc, char* argv[]) {
    unsigned mx = 200; // Upper limit for finding primes
    unsigned wid = static_cast<unsigned>(log10(static_cast<long double>(mx))) + 1; // Width for formatting output

    std::cout << "Prime numbers up to " << mx << ":\n";
    std::cout << "[" << std::setw(wid) << 2 << " "; // Print 2 as the first prime
    unsigned u = 3, p = 1; // Start checking primes from 3
    while (u <= mx) {
        if (isPrime(u)) { // Check if the number is prime
            std::cout << std::setw(wid) << u << " "; // Print the prime number
            p++; // Increment the prime count
        }
        u += 2; // Move to the next odd number for efficiency (skipping even numbers)
    }
    std::cout << "]\n\n Found " << p << " primes.\n\n"; // Display the count of primes found
    return 0;
}

Sample Output:

Prime numbers upto 200:
[  2   3   5   7  11  13  17  19  23  29  31  37  41  43  47  53  59  61  67  71  73  79  83  89  97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 ]

 Found 46 primes

Flowchart:

C++ Code Editor:

Contribute your code and comments through Disqus.

Previous: Prime decomposition.