SQL Exercise: Find the maximum penalty shots taken by the teams
25. From the following tables, write a SQL query to find the maximum penalty shots taken by the teams. Return country name, maximum penalty shots.
Sample table: soccer_country
country_id | country_abbr | country_name
------------+--------------+---------------------
1201 | ALB | Albania
1202 | AUT | Austria
1203 | BEL | Belgium
1204 | CRO | Croatia
1205 | CZE | Czech Republic
1206 | ENG | England
1207 | FRA | France
1208 | GER | Germany
1209 | HUN | Hungary
1210 | ISL | Iceland
1211 | ITA | Italy
1212 | NIR | Northern Ireland
1213 | POL | Poland
1214 | POR | Portugal
1215 | IRL | Republic of Ireland
1216 | ROU | Romania
1217 | RUS | Russia
1218 | SVK | Slovakia
1219 | ESP | Spain
1220 | SWE | Sweden
1221 | SUI | Switzerland
1222 | TUR | Turkey
1223 | UKR | Ukraine
1224 | WAL | Wales
1225 | SLO | Slovenia
1226 | NED | Netherlands
1227 | SRB | Serbia
1228 | SCO | Scotland
1229 | NOR | Norway
Sample table: penalty_shootout
kick_id | match_no | team_id | player_id | score_goal | kick_no
---------+----------+---------+-----------+------------+---------
1 | 37 | 1221 | 160467 | Y | 1
2 | 37 | 1213 | 160297 | Y | 2
3 | 37 | 1221 | 160477 | N | 3
4 | 37 | 1213 | 160298 | Y | 4
5 | 37 | 1221 | 160476 | Y | 5
6 | 37 | 1213 | 160281 | Y | 6
7 | 37 | 1221 | 160470 | Y | 7
8 | 37 | 1213 | 160287 | Y | 8
9 | 37 | 1221 | 160469 | Y | 9
10 | 37 | 1213 | 160291 | Y | 10
11 | 45 | 1214 | 160322 | Y | 1
12 | 45 | 1213 | 160297 | Y | 2
13 | 45 | 1214 | 160316 | Y | 3
14 | 45 | 1213 | 160298 | Y | 4
15 | 45 | 1214 | 160314 | Y | 5
16 | 45 | 1213 | 160281 | Y | 6
17 | 45 | 1214 | 160320 | Y | 7
18 | 45 | 1213 | 160287 | N | 8
19 | 45 | 1214 | 160321 | Y | 9
20 | 47 | 1211 | 160251 | Y | 1
21 | 47 | 1208 | 160176 | Y | 2
22 | 47 | 1211 | 160253 | N | 3
23 | 47 | 1208 | 160183 | N | 4
24 | 47 | 1211 | 160234 | Y | 5
25 | 47 | 1208 | 160177 | N | 6
26 | 47 | 1211 | 160252 | N | 7
27 | 47 | 1208 | 160173 | Y | 8
28 | 47 | 1211 | 160235 | N | 9
29 | 47 | 1208 | 160180 | N | 10
30 | 47 | 1211 | 160244 | Y | 11
31 | 47 | 1208 | 160168 | Y | 12
32 | 47 | 1211 | 160246 | Y | 13
33 | 47 | 1208 | 160169 | Y | 14
34 | 47 | 1211 | 160238 | Y | 15
35 | 47 | 1208 | 160165 | Y | 16
36 | 47 | 1211 | 160237 | N | 17
37 | 47 | 1208 | 160166 | Y | 18
Sample Solution:
SQL Code:
SELECT a.country_name, COUNT(b.*) shots
FROM soccer_country a, penalty_shootout b
WHERE b.team_id=a.country_id
GROUP BY a.country_name
having COUNT(b.*)=(
SELECT MAX(shots) FROM (
SELECT COUNT(*) shots
FROM penalty_shootout
GROUP BY team_id) inner_result);
Sample Output:
country_name | shots --------------+------- Poland | 9 Italy | 9 Germany | 9 (3 rows)
Code Explanation:
The said query in SQL that retrieves the name of the country with the highest number of penalty shootout shots taken in a soccer match.
The WHERE clause joins the two tables soccer_country and penalty_shootout using the country_id and team_id fields.
The GROUP BY clause groups the results by country name.
The HAVING clause filters the results by the highest number of penalty shootout shots. It compares the count of shots for each country to the maximum count of shots across all teams, which is obtained from a subquery that uses the GROUP BY clause to count the shots for each team.
The subquery retrieves the number of penalty shootout shots for each team, and the outer query selects the country with the highest count of shots among all teams.
Alternative Solution:
Using JOIN and Subqueries:
SELECT sc1.country_name, COUNT(ps.*) AS shots
FROM soccer_country sc1
JOIN penalty_shootout ps ON sc1.country_id = ps.team_id
GROUP BY sc1.country_name
HAVING COUNT(ps.*) = (
SELECT MAX(shots)
FROM (
SELECT COUNT(*) AS shots
FROM penalty_shootout
GROUP BY team_id
) AS inner_result
);
Explanation:
This query uses JOIN operations to connect the soccer_country table with penalty_shootout based on their respective IDs. It then applies GROUP BY and HAVING clauses to count the shots for each country and find the country with the maximum shots.
Using Subqueries with JOINs:
SELECT a.country_name, COUNT(b.*) AS shots
FROM soccer_country a
JOIN penalty_shootout b ON b.team_id = a.country_id
WHERE (
SELECT COUNT(*)
FROM penalty_shootout c
WHERE c.team_id = a.country_id
) = (
SELECT MAX(shots)
FROM (
SELECT COUNT(*) AS shots
FROM penalty_shootout
GROUP BY team_id
) inner_result
)
GROUP BY a.country_name;
Explanation:
This query uses subqueries with joins to first calculate the shots count for each team. It then applies a WHERE clause to filter the countries with the maximum shots and uses GROUP BY to count the shots for each country.
Go to:
PREV : Find the runners-up in Football EURO cup 2016.
NEXT : Find the maximum number of penalty shots taken.
Practice Online
Sample Database: soccer
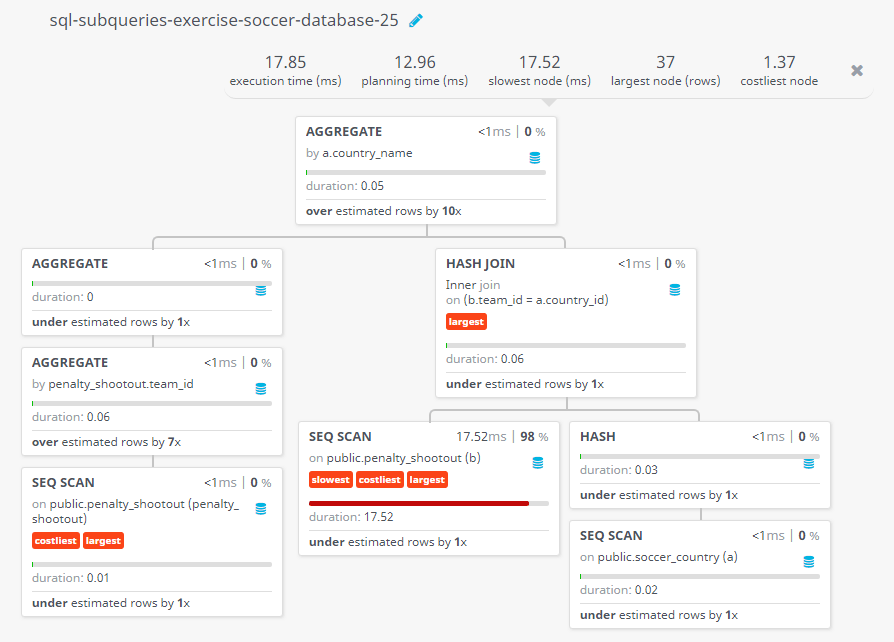
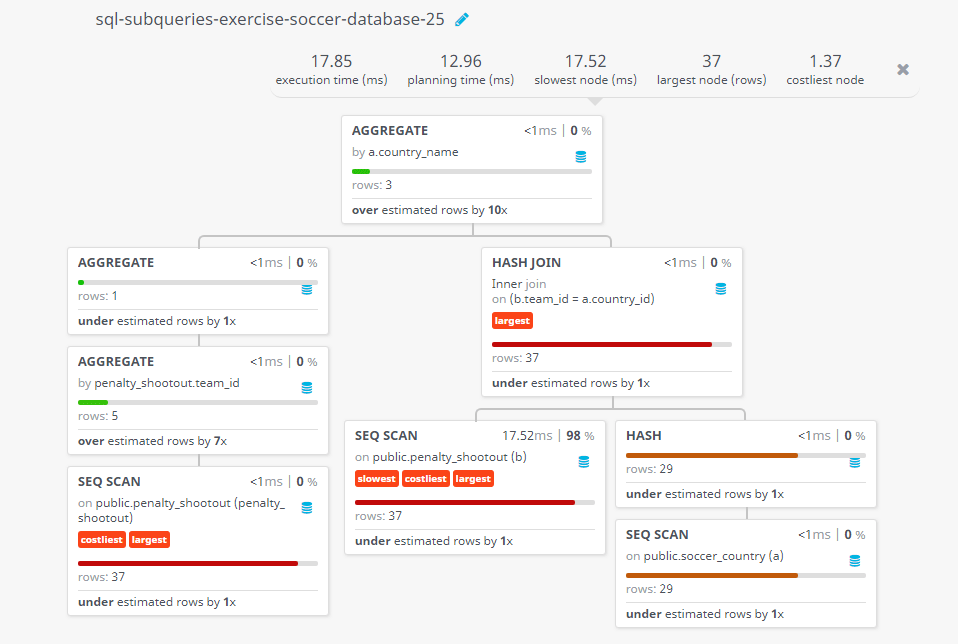
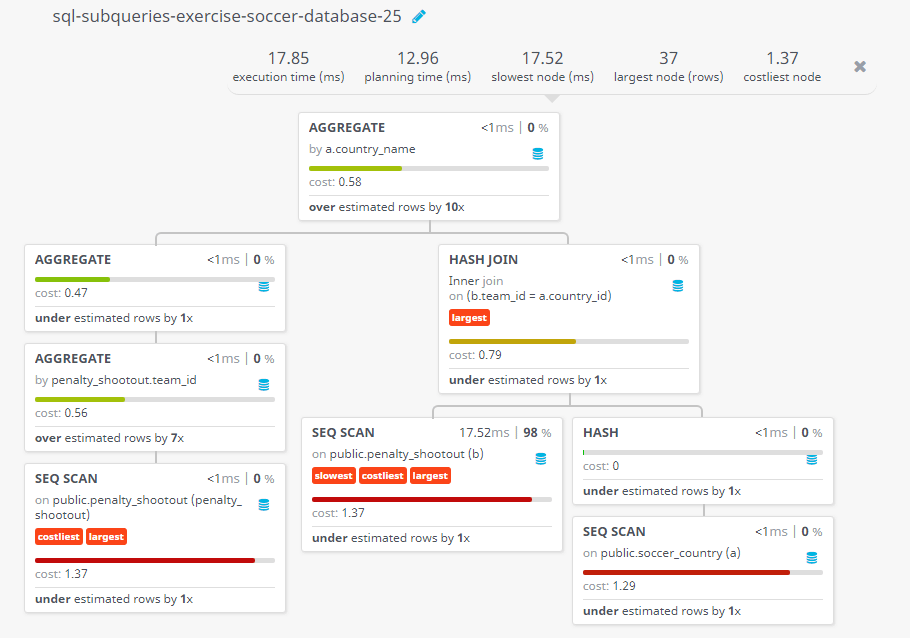
Query Visualization:
Duration:
Rows:
Cost:
Have another way to solve this solution? Contribute your code (and comments) through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.