Python: Create a symmetric difference
9. Create a Symmetric Difference
Write a Python program to create a symmetric difference.
From Wikipedia,
In mathematics, the symmetric difference, also known as the disjunctive union, of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by
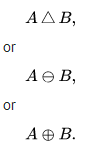
For example, the symmetric difference of the sets {1,2,3} and {3,4} is {1,2,4}.
Sample Solution-1:
Using symmetric_difference() Method
Python Code:
# Create a set 'setc1' with elements "green" and "blue":
setc1 = set(["green", "blue"])
# Create a set 'setc2' with elements "blue" and "yellow":
setc2 = set(["blue", "yellow"])
# Print a message to indicate the original sets:
print("Original sets:")
# Print the contents of 'setc1' and 'setc2':
print(setc1)
print(setc2)
# Calculate the symmetric difference of 'setc1' and 'setc2' and store it in 'r1':
r1 = setc1.symmetric_difference(setc2)
# Print a message to indicate the symmetric difference of 'setc1 - setc2':
print("\nSymmetric difference of setc1 - setc2:")
# Print the result 'r1', which contains elements that are unique to each of 'setc1' and 'setc2':
print(r1)
# Calculate the symmetric difference of 'setc2' and 'setc1' and store it in 'r2':
r2 = setc2.symmetric_difference(setc1)
# Print a message to indicate the symmetric difference of 'setc2 - setc1':
print("\nSymmetric difference of setc2 - setc1:")
# Print the result 'r2', which is the same as 'r1' and contains elements unique to each set:
print(r2)
# Create a set 'setn1' with repeated elements, including 1, 2, 3, 4, and 5:
setn1 = set([1, 1, 2, 3, 4, 5])
# Create a set 'setn2' with elements including 1, 5, 6, 7, 8, and 9:
setn2 = set([1, 5, 6, 7, 8, 9])
# Print a message to indicate the original sets:
print("\nOriginal sets:")
# Print the contents of 'setn1' and 'setn2':
print(setn1)
print(setn2)
# Calculate the symmetric difference of 'setn1' and 'setn2' and store it in 'r1':
r1 = setn1.symmetric_difference(setn2)
# Print a message to indicate the symmetric difference of 'setn1 - setn2':
print("\nSymmetric difference of setn1 - setn2:")
# Print the result 'r1', which contains elements unique to each of 'setn1' and 'setn2':
print(r1)
# Calculate the symmetric difference of 'setn2' and 'setn1' and store it in 'r2':
r2 = setn2.symmetric_difference(setn1)
# Print a message to indicate the symmetric difference of 'setn2 - setn1':
print("\nSymmetric difference of setn2 - setn1:")
# Print the result 'r2', which is the same as 'r1' and contains elements unique to each set:
print(r2)
Sample Output:
Original sets:
{'blue', 'green'}
{'blue', 'yellow'}
Symmetric difference of setc1 - setc2:
{'yellow', 'green'}
Symmetric difference of setc2 - setc1:
{'yellow', 'green'}
Original sets:
{1, 2, 3, 4, 5}
{1, 5, 6, 7, 8, 9}
Symmetric difference of setn1 - setn2:
{2, 3, 4, 6, 7, 8, 9}
Symmetric difference of setn2 - setn1:
{2, 3, 4, 6, 7, 8, 9}
Visual Presentation:
Sample Solution-2:
Using symmetric difference operator(^)
Python Code:
# Create a set 'setc1' with elements "green" and "blue":
setc1 = set(["green", "blue"])
# Create a set 'setc2' with elements "blue" and "yellow":
setc2 = set(["blue", "yellow"])
# Print a message to indicate the original sets:
print("Original sets:")
# Print the contents of 'setc1' and 'setc2':
print(setc1)
print(setc2)
# Calculate the symmetric difference of 'setc1' and 'setc2' using the '^' operator and store it in 'r1':
r1 = setc1 ^ setc2
# Print a message to indicate the symmetric difference of 'setc1 - setc2':
print("\nSymmetric difference of setc1 - setc2:")
# Print the result 'r1', which contains elements that are unique to each of 'setc1' and 'setc2':
print(r1)
# Calculate the symmetric difference of 'setc2' and 'setc1' using the '^' operator and store it in 'r2':
r2 = setc2 ^ setc1
# Print a message to indicate the symmetric difference of 'setc2 - setc1':
print("\nSymmetric difference of setc2 - setc1:")
# Print the result 'r2', which is the same as 'r1' and contains elements unique to each set:
print(r2)
# Create a set 'setn1' with repeated elements, including 1, 2, 3, 4, and 5:
setn1 = set([1, 1, 2, 3, 4, 5])
# Create a set 'setn2' with elements including 1, 5, 6, 7, 8, and 9:
setn2 = set([1, 5, 6, 7, 8, 9])
# Print a message to indicate the original sets:
print("\nOriginal sets:")
# Print the contents of 'setn1' and 'setn2':
print(setn1)
print(setn2)
# Calculate the symmetric difference of 'setn1' and 'setn2' using the '^' operator and store it in 'r1':
r1 = setn1 ^ setn2
# Print a message to indicate the symmetric difference of 'setn1 - setn2':
print("\nSymmetric difference of setn1 - setn2:")
# Print the result 'r1', which contains elements unique to each of 'setn1' and 'setn2':
print(r1)
# Calculate the symmetric difference of 'setn2' and 'setn1' using the '^' operator and store it in 'r2':
r2 = setn2 ^ setn1
# Print a message to indicate the symmetric difference of 'setn2 - setn1':
print("\nSymmetric difference of setn2 - setn1:")
# Print the result 'r2', which is the same as 'r1' and contains elements unique to each set:
print(r2)
Sample Output:
Original sets:
{'blue', 'green'}
{'yellow', 'blue'}
Symmetric difference of setc1 - setc2:
{'yellow', 'green'}
Symmetric difference of setc2 - setc1:
{'yellow', 'green'}
Original sets:
{1, 2, 3, 4, 5}
{1, 5, 6, 7, 8, 9}
Symmetric difference of setn1 - setn2:
{2, 3, 4, 6, 7, 8, 9}
Symmetric difference of setn2 - setn1:
{2, 3, 4, 6, 7, 8, 9}
Visual Presentation:
For more Practice: Solve these Related Problems:
- Write a Python program to compute the symmetric difference between two sets using the ^ operator.
- Write a Python program to use the symmetric_difference() method to get elements present in only one set.
- Write a Python program to implement a function that returns the symmetric difference of two sets as a new set.
- Write a Python program to compare two sets and output a sorted list of elements that are not common to both.
Go to:
Previous: Write a Python program to create set difference.
Next: Write a Python program to check if a set is a subset of another set.
Python Code Editor:
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
