Python: Intersection of sets

Python sets: Exercise-6 with Solution

Write a Python program to create an intersection of sets.

In mathematics, the intersection of two sets A and B, denoted by A ∩ B, is the set containing all elements of A that also belong to B (or equivalently, all elements of B that also belong to A).

In set-builder notation, A ∩ B = {x ∈ U : x ∈ A and x ∈ B}.

The Venn diagram for A ∩ B is shown to the right where the shaded region represents the set A ∩ B.

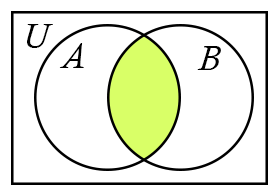
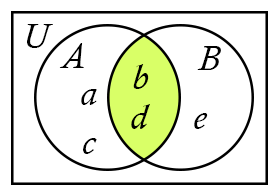
Example: Let A = {a, b, c, d} and B = {b, d, e}. Then A ∩ B = {b, d}. The elements b and d are the only elements that are in both sets A and B.

Visual Presentation:

Sample Solution-1:

Python Code:

# Create a set 'setx' with elements "green" and "blue":
setx = set(["green", "blue"])

# Create a set 'sety' with elements "blue" and "yellow":
sety = set(["blue", "yellow"])

# Print a message to indicate the original set elements:
print("Original set elements:")

# Print the contents of 'setx':
print(setx)

# Print the contents of 'sety':
print(sety)

# Print a message to indicate the intersection of the two sets:
print("\nIntersection of two said sets:")

# Find the intersection of 'setx' and 'sety' and store it in 'setz':
setz = setx & sety

# Print the resulting 'setz', which contains elements that are common to both 'setx' and 'sety':
print(setz)

Sample Output:

Original set elements:
{'green', 'blue'}
{'blue', 'yellow'}

Intersection of two said sets:
{'blue'}

Sample Solution-2:

Python Code:

# Define a function 'intersection_of_sets' that takes two sets 'sc1' and 'sc2' as arguments:
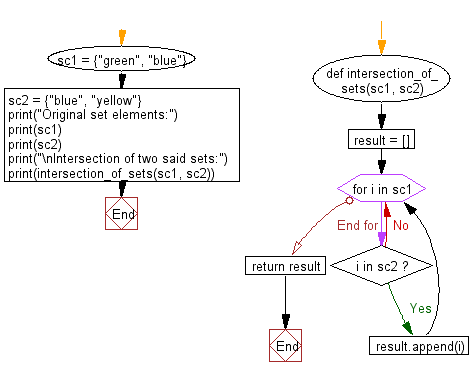
def intersection_of_sets(sc1, sc2):
    # Create an empty list 'result' to store the common elements:
    result = []
    
    # Iterate through the elements in 'sc1':
    for i in sc1:
        # Check if the current element 'i' is also present in 'sc2':
        if i in sc2:
            # If 'i' is in both sets, add it to the 'result' list:
            result.append(i)
    
    # Return the 'result' list containing the common elements:
    return result

# Create a set 'sc1' with elements "green" and "blue":
sc1 = {"green", "blue"}

# Create a set 'sc2' with elements "blue" and "yellow":
sc2 = {"blue", "yellow"}

# Print a message to indicate the original set elements:
print("Original set elements:")

# Print the contents of 'sc1':
print(sc1)

# Print the contents of 'sc2':
print(sc2)

# Print a message to indicate the intersection of the two sets:
print("\nIntersection of two said sets:")

# Call the 'intersection_of_sets' function with 'sc1' and 'sc2' as arguments and print the result:
print(intersection_of_sets(sc1, sc2)) 

Sample Output:

Original set elements:
{'green', 'blue'}
{'yellow', 'blue'}

Intersection of two said sets:
['blue']

Flowchart:

Sample Solution-3:

Python Code:

# Create a set 'setx' with elements "green" and "blue":
setx = set(["green", "blue"])

# Create a set 'sety' with elements "blue" and "yellow":
sety = set(["blue", "yellow"])

# Print a message to indicate the original set elements:
print("Original set elements:")

# Print the contents of 'setx':
print(setx)

# Print the contents of 'sety':
print(sety)

# Print a message to indicate the intersection of the two sets:
print("\nIntersection of two said sets:")

# Use the 'intersection' method to find the intersection of 'setx' and 'sety' and store it in the 'result' set:
result = setx.intersection(sety)

# Print the resulting 'result' set, which contains elements that are common to both 'setx' and 'sety':
print(result) 

Sample Output:

Original set elements:
{'green', 'blue'}
{'yellow', 'blue'}

Intersection of two said sets:
['blue']

Python Code Editor:

Previous: Write a Python program to remove an item from a set if it is present in the set.
Next: Write a Python program to create a union of sets.