Python Exercise: Test the number is prime or not

Last update on April 22 2025 12:58:09 (UTC/GMT +8 hours)

9. Check Whether a Number is Prime

Write a Python function that takes a number as a parameter and checks whether the number is prime or not.

Note : A prime number (or a prime) is a natural number greater than 1 and that has no positive divisors other than 1 and itself.

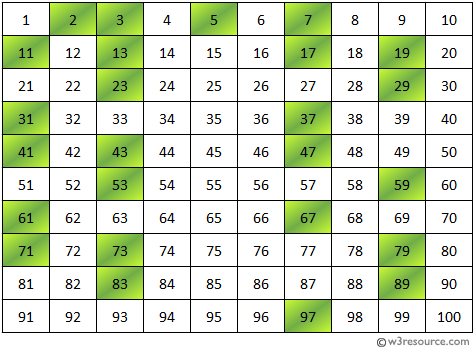
Prime number between 1 to 100:

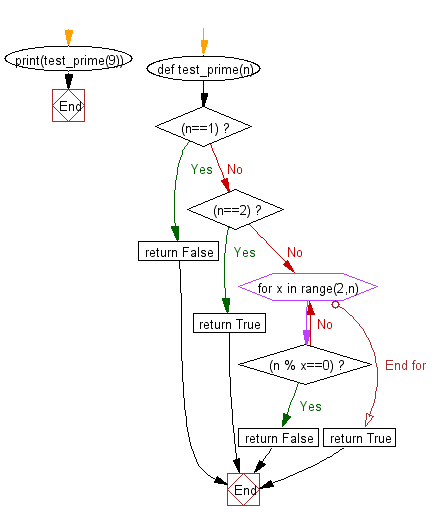
Sample Solution-1:

Python Code:

# Define a function named 'test_prime' that checks if a number 'n' is a prime number
def test_prime(n):
    # Check if 'n' is equal to 1
    if (n == 1):
        # If 'n' is 1, return False (1 is not a prime number)
        return False
    # Check if 'n' is equal to 2
    elif (n == 2):
        # If 'n' is 2, return True (2 is a prime number)
        return True
    else:
        # Iterate through numbers from 2 to (n-1) using 'x' as the iterator
        for x in range(2, n):
            # Check if 'n' is divisible by 'x' without any remainder
            if (n % x == 0):
                # If 'n' is divisible by 'x', return False (not a prime number)
                return False
        # If 'n' is not divisible by any number from 2 to (n-1), return True (prime number)
        return True

# Print the result of checking if 9 is a prime number by calling the 'test_prime' function
print(test_prime(9))

Sample Output:

False

Explanation:

In the exercise above the code defines a function named "test_prime()" that determines whether a given number 'n' is a prime number or not. It performs various checks such as excluding 1 as a prime number, including 2 as a prime number, and then checks the divisibility from 2 to 'n-1'. Finally, it demonstrates the function by calling it with the argument 9 and prints the result (False) indicating that 9 is not a prime number.

Flowchart:

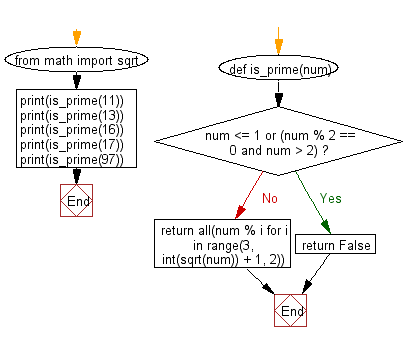
Sample Solution-2:

Return False if the number is 0, 1, a negative number or a multiple of 2.
Use all() and range() to check numbers from 3 to the square root of the given number.
Return True if none divides the given number, False otherwise.

Python Code:

# Import the 'sqrt' function from the 'math' module
from math import sqrt

# Define a function named 'is_prime' that checks if a number 'num' is a prime number
def is_prime(num):
    # Check conditions:
    # If 'num' is less than or equal to 1 or if 'num' is even and greater than 2, return False
    if num <= 1 or (num % 2 == 0 and num > 2): 
        return False
    
    # Check if 'num' is divisible by any odd number from 3 to the square root of 'num'
    # If any number from this range divides 'num' evenly, return False; otherwise, return True
    return all(num % i for i in range(3, int(sqrt(num)) + 1, 2))

# Print the result of checking whether certain numbers are prime by calling the 'is_prime' function
print(is_prime(11))
print(is_prime(13))
print(is_prime(16))
print(is_prime(17))
print(is_prime(97))

Sample Output:

True
True
False
True
True

Explanation:

In the exercise above the code defines a function named "is_prime()" that checks whether a given number 'num' is a prime number. It checks various conditions, such as excluding numbers less than or equal to 1, even numbers greater than 2, and then checks divisibility by odd numbers from 3 to the square root of 'num'. Finally, it calls the function with different numbers and prints the results indicating whether they are prime (True) or not (False).

Flowchart:

For more Practice: Solve these Related Problems:

Write a Python function that determines if a number is prime by checking divisibility from 2 up to the square root of the number.
Write a Python function that uses recursion to determine whether a given number is prime.
Write a Python function that employs a for-loop with an early exit upon finding a divisor, then returns True or False.
Write a Python function that uses a list comprehension to generate potential divisors and checks if the list is empty to confirm primality.

Go to:

Previous: Write a Python function that takes a list and returns a new list with unique elements of the first list.
Next: Write a Python program to print the even numbers from a given list.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.