w3resource

Python: Find all integers that are the product of exactly three primes

Integers as Product of Three Primes

Write a Python program to find all integers <= 1000 that are the product of exactly three primes. Each integer should be represented as a list of its three prime factors.

Input: 
10
Output:
[[2, 2, 2]]

Input: 
50
Output:
[[2, 2, 2], [2, 2, 3], [2, 2, 5], [2, 2, 7], [2, 2, 11], [2, 3, 2], [2, 3, 3], [2, 3, 5], [2, 3, 7], [2, 5, 2], [2, 5, 3], [2, 5, 5], [2, 7, 2], [2, 7, 3], [2, 11, 2], [3, 2, 2], [3, 2, 3], [3, 2, 5], [3, 2, 7], [3, 3, 2], [3, 3, 3], [3, 3, 5], [3, 5, 2], [3, 5, 3], [3, 7, 2], [5, 2, 2], [5, 2, 3], [5, 2, 5], [5, 3, 2], [5, 3, 3], [5, 5, 2], [7, 2, 2], [7, 2, 3], [7, 3, 2], [11, 2, 2]]

Visual Presentation:

Python: Find all integers that are the product of exactly three primes.

Sample Solution:

Python Code:

# License: https://bit.ly/3oLErEI

# Define a function named 'test' that takes an integer parameter 'n'
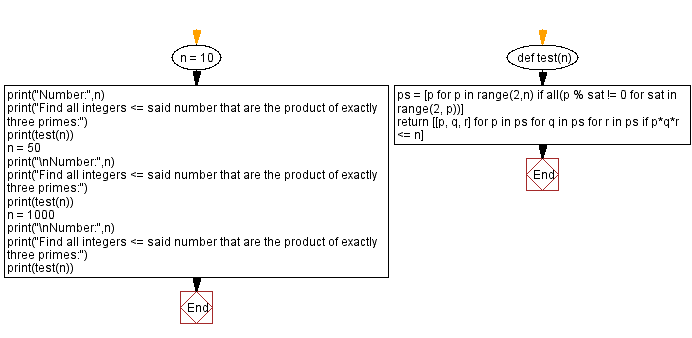
def test(n):    
    # Generate a list 'ps' containing all prime numbers less than 'n'
    ps = [p for p in range(2, n) if all(p % sat != 0 for sat in range(2, p))]
    
    # Generate a list of lists containing all integers <= 'n' that are the product of exactly three primes
    return [[p, q, r] for p in ps for q in ps for r in ps if p * q * r <= n]   

# Example 1
n1 = 10
print("Number:", n1)
print("Find all integers <= said number that are the product of exactly three primes:")
print(test(n1))

# Example 2
n2 = 50
print("\nNumber:", n2)
print("Find all integers <= said number that are the product of exactly three primes:")
print(test(n2))

# Example 3
n3 = 1000
print("\nNumber:", n3)
print("Find all integers <= said number that are the product of exactly three primes:")
print(test(n3))

Sample Output:

Number: 10
Find all integers <= said number that are the product of exactly three primes:
[[2, 2, 2]]

Number: 50
Find all integers <= said number that are the product of exactly three primes:
[[2, 2, 2], [2, 2, 3], [2, 2, 5], [2, 2, 7], [2, 2, 11], [2, 3, 2], [2, 3, 3], [2, 3, 5], [2, 3, 7], [2, 5, 2], [2, 5, 3], [2, 5, 5], [2, 7, 2], [2, 7, 3], [2, 11, 2], [3, 2, 2], [3, 2, 3], [3, 2, 5], [3, 2, 7], [3, 3, 2], [3, 3, 3], [3, 3, 5], [3, 5, 2], [3, 5, 3], [3, 7, 2], [5, 2, 2], [5, 2, 3], [5, 2, 5], [5, 3, 2], [5, 3, 3], [5, 5, 2], [7, 2, 2], [7, 2, 3], [7, 3, 2], [11, 2, 2]]

Number: 1000
Find all integers <= said number that are the product of exactly three primes:
[[2, 2, 2], [2, 2, 3], [2, 2, 5], [2, 2, 7], [2, 2, 11], [2, 2, 13], [2, 2, 17], [2, 2, 19], [2, 2, 23], [2, 2, 29], [2, 2, 31], [2, 2, 37], [2, 2, 41], [2, 2, 43], [2, 2, 47], [2, 2, 53], [2, 2, 59], [2, 2, 61], [2, 2, 67], [2, 2, 71], [2, 2, 73], [2, 2, 79], [2, 2, 83], [2, 2, 89], [2, 2, 97], [2, 2, 101], [2, 2, 103], [2, 2, 107], [2, 2, 109], [2, 2, 113], [2, 2, 127], [2, 2, 131], [2, 2, 137], [2, 2, 139], [2, 2, 149], [2, 2, 151], [2, 2, 157], [2, 2, 163], [2, 2, 167], [2, 2, 173], [2, 2, 179], [2, 2, 181], [2, 2, 191], [2, 2, 193], [2, 2, 197], [2, 2, 199], [2, 2, 211], [2, 2, 223], [2, 2, 227], [2, 2, 229], [2, 2, 233], [2, 2, 239], [2, 2, 241], [2, 3, 2], [2, 3, 3], [2, 3, 5], [2, 3, 7], [2, 3, 11], [2, 3, 13], [2, 3, 17], [2, 3, 19], [2, 3, 23], [2, 3, 29], [2, 3, 31], [2, 3, 37], [2, 3, 41], [2, 3, 43], [2, 3, 47], [2, 3, 53], [2, 3, 59], [2, 3, 61], [2, 3, 67], [2, 3, 71], [2, 3, 73], [2, 3, 79], [2, 3, 83], [2, 3, 89], [2, 3, 97], [2, 3, 101], [2, 3, 103], [2, 3, 107], [2, 3, 109], [2, 3, 113], [2, 3, 127], [2, 3, 131], [2, 3, 137], [2, 3, 139], [2, 3, 149], [2, 3, 151], [2, 3, 157], [2, 3, 163], [2, 5, 2], [2, 5, 3], [2, 5, 5], [2, 5, 7], [2, 5, 11], [2, 5, 13], [2, 5, 17], [2, 5, 19], [2, 5, 23], [2, 5, 29], [2, 5, 31], [2, 5, 37], [2, 5, 41], [2, 5, 43], [2, 5, 47], [2, 5, 53], [2, 5, 59], [2, 5, 61], [2, 5, 67], [2, 5, 71], [2, 5, 73], [2, 5, 79], [2, 5, 83], [2, 5, 89], [2, 5, 97], [2, 7, 2], [2, 7, 3], [2, 7, 5], [2, 7, 7], [2, 7, 11], [2, 7, 13], [2, 7, 17], [2, 7, 19], [2, 7, 23], [2, 7, 29], [2, 7, 31], [2, 7, 37], [2, 7, 41], [2, 7, 43], [2, 7, 47], [2, 7, 53], [2, 7, 59], [2, 7, 61], [2, 7, 67], [2, 7, 71], [2, 11, 2], [2, 11, 3], [2, 11, 5], [2, 11, 7], [2, 11, 11], [2, 11, 13], [2, 11, 17], [2, 11, 19], [2, 11, 23], [2, 11, 29], [2, 11, 31], [2, 11, 37], [2, 11, 41], [2, 11, 43], [2, 13, 2], [2, 13, 3], [2, 13, 5], [2, 13, 7], [2, 13, 11], [2, 13, 13], [2, 13, 17], [2, 13, 19], [2, 13, 23], [2, 13, 29], [2, 13, 31], [2, 13, 37], [2, 17, 2], [2, 17, 3], [2, 17, 5], [2, 17, 7], [2, 17, 11], [2, 17, 13], [2, 17, 17], [2, 17, 19], [2, 17, 23], [2, 17, 29], [2, 19, 2], [2, 19, 3], [2, 19, 5], [2, 19, 7], [2, 19, 11], [2, 19, 13], [2, 19, 17], [2, 19, 19], [2, 19, 23], [2, 23, 2], [2, 23, 3], [2, 23, 5], [2, 23, 7], [2, 23, 11], [2, 23, 13], [2, 23, 17], [2, 23, 19], [2, 29, 2], [2, 29, 3], [2, 29, 5], [2, 29, 7], [2, 29, 11], [2, 29, 13], [2, 29, 17], [2, 31, 2], [2, 31, 3], [2, 31, 5], [2, 31, 7], [2, 31, 11], [2, 31, 13], [2, 37, 2], [2, 37, 3], [2, 37, 5], [2, 37, 7], [2, 37, 11], [2, 37, 13], [2, 41, 2], [2, 41, 3], [2, 41, 5], [2, 41, 7], [2, 41, 11], [2, 43, 2], [2, 43, 3], [2, 43, 5], [2, 43, 7], [2, 43, 11], [2, 47, 2], [2, 47, 3], [2, 47, 5], [2, 47, 7], [2, 53, 2], [2, 53, 3], [2, 53, 5], [2, 53, 7], [2, 59, 2], [2, 59, 3], [2, 59, 5], [2, 59, 7], [2, 61, 2], [2, 61, 3], [2, 61, 5], [2, 61, 7], [2, 67, 2], [2, 67, 3], [2, 67, 5], [2, 67, 7], [2, 71, 2], [2, 71, 3], [2, 71, 5], [2, 71, 7], [2, 73, 2], [2, 73, 3], [2, 73, 5], [2, 79, 2], [2, 79, 3], [2, 79, 5], [2, 83, 2], [2, 83, 3], [2, 83, 5], [2, 89, 2], [2, 89, 3], [2, 89, 5], [2, 97, 2], [2, 97, 3], [2, 97, 5], [2, 101, 2], [2, 101, 3], [2, 103, 2], [2, 103, 3], [2, 107, 2], [2, 107, 3], [2, 109, 2], [2, 109, 3], [2, 113, 2], [2, 113, 3], [2, 127, 2], [2, 127, 3], [2, 131, 2], [2, 131, 3], [2, 137, 2], [2, 137, 3], [2, 139, 2], [2, 139, 3], [2, 149, 2], [2, 149, 3], [2, 151, 2], [2, 151, 3], [2, 157, 2], [2, 157, 3], [2, 163, 2], [2, 163, 3], [2, 167, 2], [2, 173, 2], [2, 179, 2], [2, 181, 2], [2, 191, 2], [2, 193, 2], [2, 197, 2], [2, 199, 2], [2, 211, 2], [2, 223, 2], [2, 227, 2], [2, 229, 2], [2, 233, 2], [2, 239, 2], [2, 241, 2], [3, 2, 2], [3, 2, 3], [3, 2, 5], [3, 2, 7], [3, 2, 11], [3, 2, 13], [3, 2, 17], [3, 2, 19], [3, 2, 23], [3, 2, 29], [3, 2, 31], [3, 2, 37], [3, 2, 41], [3, 2, 43], [3, 2, 47], [3, 2, 53], [3, 2, 59], [3, 2, 61], [3, 2, 67], [3, 2, 71], [3, 2, 73], [3, 2, 79], [3, 2, 83], [3, 2, 89], [3, 2, 97], [3, 2, 101], [3, 2, 103], [3, 2, 107], [3, 2, 109], [3, 2, 113], [3, 2, 127], [3, 2, 131], [3, 2, 137], [3, 2, 139], [3, 2, 149], [3, 2, 151], [3, 2, 157], [3, 2, 163], [3, 3, 2], [3, 3, 3], [3, 3, 5], [3, 3, 7], [3, 3, 11], [3, 3, 13], [3, 3, 17], [3, 3, 19], [3, 3, 23], [3, 3, 29], [3, 3, 31], [3, 3, 37], [3, 3, 41], [3, 3, 43], [3, 3, 47], [3, 3, 53], [3, 3, 59], [3, 3, 61], [3, 3, 67], [3, 3, 71], [3, 3, 73], [3, 3, 79], [3, 3, 83], [3, 3, 89], [3, 3, 97], [3, 3, 101], [3, 3, 103], [3, 3, 107], [3, 3, 109], [3, 5, 2], [3, 5, 3], [3, 5, 5], [3, 5, 7], [3, 5, 11], [3, 5, 13], [3, 5, 17], [3, 5, 19], [3, 5, 23], [3, 5, 29], [3, 5, 31], [3, 5, 37], [3, 5, 41], [3, 5, 43], [3, 5, 47], [3, 5, 53], [3, 5, 59], [3, 5, 61], [3, 7, 2], [3, 7, 3], [3, 7, 5], [3, 7, 7], [3, 7, 11], [3, 7, 13], [3, 7, 17], [3, 7, 19], [3, 7, 23], [3, 7, 29], [3, 7, 31], [3, 7, 37], [3, 7, 41], [3, 7, 43], [3, 7, 47], [3, 11, 2], [3, 11, 3], [3, 11, 5], [3, 11, 7], [3, 11, 11], [3, 11, 13], [3, 11, 17], [3, 11, 19], [3, 11, 23], [3, 11, 29], [3, 13, 2], [3, 13, 3], [3, 13, 5], [3, 13, 7], [3, 13, 11], [3, 13, 13], [3, 13, 17], [3, 13, 19], [3, 13, 23], [3, 17, 2], [3, 17, 3], [3, 17, 5], [3, 17, 7], [3, 17, 11], [3, 17, 13], [3, 17, 17], [3, 17, 19], [3, 19, 2], [3, 19, 3], [3, 19, 5], [3, 19, 7], [3, 19, 11], [3, 19, 13], [3, 19, 17], [3, 23, 2], [3, 23, 3], [3, 23, 5], [3, 23, 7], [3, 23, 11], [3, 23, 13], [3, 29, 2], [3, 29, 3], [3, 29, 5], [3, 29, 7], [3, 29, 11], [3, 31, 2], [3, 31, 3], [3, 31, 5], [3, 31, 7], [3, 37, 2], [3, 37, 3], [3, 37, 5], [3, 37, 7], [3, 41, 2], [3, 41, 3], [3, 41, 5], [3, 41, 7], [3, 43, 2], [3, 43, 3], [3, 43, 5], [3, 43, 7], [3, 47, 2], [3, 47, 3], [3, 47, 5], [3, 47, 7], [3, 53, 2], [3, 53, 3], [3, 53, 5], [3, 59, 2], [3, 59, 3], [3, 59, 5], [3, 61, 2], [3, 61, 3], [3, 61, 5], [3, 67, 2], [3, 67, 3], [3, 71, 2], [3, 71, 3], [3, 73, 2], [3, 73, 3], [3, 79, 2], [3, 79, 3], [3, 83, 2], [3, 83, 3], [3, 89, 2], [3, 89, 3], [3, 97, 2], [3, 97, 3], [3, 101, 2], [3, 101, 3], [3, 103, 2], [3, 103, 3], [3, 107, 2], [3, 107, 3], [3, 109, 2], [3, 109, 3], [3, 113, 2], [3, 127, 2], [3, 131, 2], [3, 137, 2], [3, 139, 2], [3, 149, 2], [3, 151, 2], [3, 157, 2], [3, 163, 2], [5, 2, 2], [5, 2, 3], [5, 2, 5], [5, 2, 7], [5, 2, 11], [5, 2, 13], [5, 2, 17], [5, 2, 19], [5, 2, 23], [5, 2, 29], [5, 2, 31], [5, 2, 37], [5, 2, 41], [5, 2, 43], [5, 2, 47], [5, 2, 53], [5, 2, 59], [5, 2, 61], [5, 2, 67], [5, 2, 71], [5, 2, 73], [5, 2, 79], [5, 2, 83], [5, 2, 89], [5, 2, 97], [5, 3, 2], [5, 3, 3], [5, 3, 5], [5, 3, 7], [5, 3, 11], [5, 3, 13], [5, 3, 17], [5, 3, 19], [5, 3, 23], [5, 3, 29], [5, 3, 31], [5, 3, 37], [5, 3, 41], [5, 3, 43], [5, 3, 47], [5, 3, 53], [5, 3, 59], [5, 3, 61], [5, 5, 2], [5, 5, 3], [5, 5, 5], [5, 5, 7], [5, 5, 11], [5, 5, 13], [5, 5, 17], [5, 5, 19], [5, 5, 23], [5, 5, 29], [5, 5, 31], [5, 5, 37], [5, 7, 2], [5, 7, 3], [5, 7, 5], [5, 7, 7], [5, 7, 11], [5, 7, 13], [5, 7, 17], [5, 7, 19], [5, 7, 23], [5, 11, 2], [5, 11, 3], [5, 11, 5], [5, 11, 7], [5, 11, 11], [5, 11, 13], [5, 11, 17], [5, 13, 2], [5, 13, 3], [5, 13, 5], [5, 13, 7], [5, 13, 11], [5, 13, 13], [5, 17, 2], [5, 17, 3], [5, 17, 5], [5, 17, 7], [5, 17, 11], [5, 19, 2], [5, 19, 3], [5, 19, 5], [5, 19, 7], [5, 23, 2], [5, 23, 3], [5, 23, 5], [5, 23, 7], [5, 29, 2], [5, 29, 3], [5, 29, 5], [5, 31, 2], [5, 31, 3], [5, 31, 5], [5, 37, 2], [5, 37, 3], [5, 37, 5], [5, 41, 2], [5, 41, 3], [5, 43, 2], [5, 43, 3], [5, 47, 2], [5, 47, 3], [5, 53, 2], [5, 53, 3], [5, 59, 2], [5, 59, 3], [5, 61, 2], [5, 61, 3], [5, 67, 2], [5, 71, 2], [5, 73, 2], [5, 79, 2], [5, 83, 2], [5, 89, 2], [5, 97, 2], [7, 2, 2], [7, 2, 3], [7, 2, 5], [7, 2, 7], [7, 2, 11], [7, 2, 13], [7, 2, 17], [7, 2, 19], [7, 2, 23], [7, 2, 29], [7, 2, 31], [7, 2, 37], [7, 2, 41], [7, 2, 43], [7, 2, 47], [7, 2, 53], [7, 2, 59], [7, 2, 61], [7, 2, 67], [7, 2, 71], [7, 3, 2], [7, 3, 3], [7, 3, 5], [7, 3, 7], [7, 3, 11], [7, 3, 13], [7, 3, 17], [7, 3, 19], [7, 3, 23], [7, 3, 29], [7, 3, 31], [7, 3, 37], [7, 3, 41], [7, 3, 43], [7, 3, 47], [7, 5, 2], [7, 5, 3], [7, 5, 5], [7, 5, 7], [7, 5, 11], [7, 5, 13], [7, 5, 17], [7, 5, 19], [7, 5, 23], [7, 7, 2], [7, 7, 3], [7, 7, 5], [7, 7, 7], [7, 7, 11], [7, 7, 13], [7, 7, 17], [7, 7, 19], [7, 11, 2], [7, 11, 3], [7, 11, 5], [7, 11, 7], [7, 11, 11], [7, 13, 2], [7, 13, 3], [7, 13, 5], [7, 13, 7], [7, 17, 2], [7, 17, 3], [7, 17, 5], [7, 17, 7], [7, 19, 2], [7, 19, 3], [7, 19, 5], [7, 19, 7], [7, 23, 2], [7, 23, 3], [7, 23, 5], [7, 29, 2], [7, 29, 3], [7, 31, 2], [7, 31, 3], [7, 37, 2], [7, 37, 3], [7, 41, 2], [7, 41, 3], [7, 43, 2], [7, 43, 3], [7, 47, 2], [7, 47, 3], [7, 53, 2], [7, 59, 2], [7, 61, 2], [7, 67, 2], [7, 71, 2], [11, 2, 2], [11, 2, 3], [11, 2, 5], [11, 2, 7], [11, 2, 11], [11, 2, 13], [11, 2, 17], [11, 2, 19], [11, 2, 23], [11, 2, 29], [11, 2, 31], [11, 2, 37], [11, 2, 41], [11, 2, 43], [11, 3, 2], [11, 3, 3], [11, 3, 5], [11, 3, 7], [11, 3, 11], [11, 3, 13], [11, 3, 17], [11, 3, 19], [11, 3, 23], [11, 3, 29], [11, 5, 2], [11, 5, 3], [11, 5, 5], [11, 5, 7], [11, 5, 11], [11, 5, 13], [11, 5, 17], [11, 7, 2], [11, 7, 3], [11, 7, 5], [11, 7, 7], [11, 7, 11], [11, 11, 2], [11, 11, 3], [11, 11, 5], [11, 11, 7], [11, 13, 2], [11, 13, 3], [11, 13, 5], [11, 17, 2], [11, 17, 3], [11, 17, 5], [11, 19, 2], [11, 19, 3], [11, 23, 2], [11, 23, 3], [11, 29, 2], [11, 29, 3], [11, 31, 2], [11, 37, 2], [11, 41, 2], [11, 43, 2], [13, 2, 2], [13, 2, 3], [13, 2, 5], [13, 2, 7], [13, 2, 11], [13, 2, 13], [13, 2, 17], [13, 2, 19], [13, 2, 23], [13, 2, 29], [13, 2, 31], [13, 2, 37], [13, 3, 2], [13, 3, 3], [13, 3, 5], [13, 3, 7], [13, 3, 11], [13, 3, 13], [13, 3, 17], [13, 3, 19], [13, 3, 23], [13, 5, 2], [13, 5, 3], [13, 5, 5], [13, 5, 7], [13, 5, 11], [13, 5, 13], [13, 7, 2], [13, 7, 3], [13, 7, 5], [13, 7, 7], [13, 11, 2], [13, 11, 3], [13, 11, 5], [13, 13, 2], [13, 13, 3], [13, 13, 5], [13, 17, 2], [13, 17, 3], [13, 19, 2], [13, 19, 3], [13, 23, 2], [13, 23, 3], [13, 29, 2], [13, 31, 2], [13, 37, 2], [17, 2, 2], [17, 2, 3], [17, 2, 5], [17, 2, 7], [17, 2, 11], [17, 2, 13], [17, 2, 17], [17, 2, 19], [17, 2, 23], [17, 2, 29], [17, 3, 2], [17, 3, 3], [17, 3, 5], [17, 3, 7], [17, 3, 11], [17, 3, 13], [17, 3, 17], [17, 3, 19], [17, 5, 2], [17, 5, 3], [17, 5, 5], [17, 5, 7], [17, 5, 11], [17, 7, 2], [17, 7, 3], [17, 7, 5], [17, 7, 7], [17, 11, 2], [17, 11, 3], [17, 11, 5], [17, 13, 2], [17, 13, 3], [17, 17, 2], [17, 17, 3], [17, 19, 2], [17, 19, 3], [17, 23, 2], [17, 29, 2], [19, 2, 2], [19, 2, 3], [19, 2, 5], [19, 2, 7], [19, 2, 11], [19, 2, 13], [19, 2, 17], [19, 2, 19], [19, 2, 23], [19, 3, 2], [19, 3, 3], [19, 3, 5], [19, 3, 7], [19, 3, 11], [19, 3, 13], [19, 3, 17], [19, 5, 2], [19, 5, 3], [19, 5, 5], [19, 5, 7], [19, 7, 2], [19, 7, 3], [19, 7, 5], [19, 7, 7], [19, 11, 2], [19, 11, 3], [19, 13, 2], [19, 13, 3], [19, 17, 2], [19, 17, 3], [19, 19, 2], [19, 23, 2], [23, 2, 2], [23, 2, 3], [23, 2, 5], [23, 2, 7], [23, 2, 11], [23, 2, 13], [23, 2, 17], [23, 2, 19], [23, 3, 2], [23, 3, 3], [23, 3, 5], [23, 3, 7], [23, 3, 11], [23, 3, 13], [23, 5, 2], [23, 5, 3], [23, 5, 5], [23, 5, 7], [23, 7, 2], [23, 7, 3], [23, 7, 5], [23, 11, 2], [23, 11, 3], [23, 13, 2], [23, 13, 3], [23, 17, 2], [23, 19, 2], [29, 2, 2], [29, 2, 3], [29, 2, 5], [29, 2, 7], [29, 2, 11], [29, 2, 13], [29, 2, 17], [29, 3, 2], [29, 3, 3], [29, 3, 5], [29, 3, 7], [29, 3, 11], [29, 5, 2], [29, 5, 3], [29, 5, 5], [29, 7, 2], [29, 7, 3], [29, 11, 2], [29, 11, 3], [29, 13, 2], [29, 17, 2], [31, 2, 2], [31, 2, 3], [31, 2, 5], [31, 2, 7], [31, 2, 11], [31, 2, 13], [31, 3, 2], [31, 3, 3], [31, 3, 5], [31, 3, 7], [31, 5, 2], [31, 5, 3], [31, 5, 5], [31, 7, 2], [31, 7, 3], [31, 11, 2], [31, 13, 2], [37, 2, 2], [37, 2, 3], [37, 2, 5], [37, 2, 7], [37, 2, 11], [37, 2, 13], [37, 3, 2], [37, 3, 3], [37, 3, 5], [37, 3, 7], [37, 5, 2], [37, 5, 3], [37, 5, 5], [37, 7, 2], [37, 7, 3], [37, 11, 2], [37, 13, 2], [41, 2, 2], [41, 2, 3], [41, 2, 5], [41, 2, 7], [41, 2, 11], [41, 3, 2], [41, 3, 3], [41, 3, 5], [41, 3, 7], [41, 5, 2], [41, 5, 3], [41, 7, 2], [41, 7, 3], [41, 11, 2], [43, 2, 2], [43, 2, 3], [43, 2, 5], [43, 2, 7], [43, 2, 11], [43, 3, 2], [43, 3, 3], [43, 3, 5], [43, 3, 7], [43, 5, 2], [43, 5, 3], [43, 7, 2], [43, 7, 3], [43, 11, 2], [47, 2, 2], [47, 2, 3], [47, 2, 5], [47, 2, 7], [47, 3, 2], [47, 3, 3], [47, 3, 5], [47, 3, 7], [47, 5, 2], [47, 5, 3], [47, 7, 2], [47, 7, 3], [53, 2, 2], [53, 2, 3], [53, 2, 5], [53, 2, 7], [53, 3, 2], [53, 3, 3], [53, 3, 5], [53, 5, 2], [53, 5, 3], [53, 7, 2], [59, 2, 2], [59, 2, 3], [59, 2, 5], [59, 2, 7], [59, 3, 2], [59, 3, 3], [59, 3, 5], [59, 5, 2], [59, 5, 3], [59, 7, 2], [61, 2, 2], [61, 2, 3], [61, 2, 5], [61, 2, 7], [61, 3, 2], [61, 3, 3], [61, 3, 5], [61, 5, 2], [61, 5, 3], [61, 7, 2], [67, 2, 2], [67, 2, 3], [67, 2, 5], [67, 2, 7], [67, 3, 2], [67, 3, 3], [67, 5, 2], [67, 7, 2], [71, 2, 2], [71, 2, 3], [71, 2, 5], [71, 2, 7], [71, 3, 2], [71, 3, 3], [71, 5, 2], [71, 7, 2], [73, 2, 2], [73, 2, 3], [73, 2, 5], [73, 3, 2], [73, 3, 3], [73, 5, 2], [79, 2, 2], [79, 2, 3], [79, 2, 5], [79, 3, 2], [79, 3, 3], [79, 5, 2], [83, 2, 2], [83, 2, 3], [83, 2, 5], [83, 3, 2], [83, 3, 3], [83, 5, 2], [89, 2, 2], [89, 2, 3], [89, 2, 5], [89, 3, 2], [89, 3, 3], [89, 5, 2], [97, 2, 2], [97, 2, 3], [97, 2, 5], [97, 3, 2], [97, 3, 3], [97, 5, 2], [101, 2, 2], [101, 2, 3], [101, 3, 2], [101, 3, 3], [103, 2, 2], [103, 2, 3], [103, 3, 2], [103, 3, 3], [107, 2, 2], [107, 2, 3], [107, 3, 2], [107, 3, 3], [109, 2, 2], [109, 2, 3], [109, 3, 2], [109, 3, 3], [113, 2, 2], [113, 2, 3], [113, 3, 2], [127, 2, 2], [127, 2, 3], [127, 3, 2], [131, 2, 2], [131, 2, 3], [131, 3, 2], [137, 2, 2], [137, 2, 3], [137, 3, 2], [139, 2, 2], [139, 2, 3], [139, 3, 2], [149, 2, 2], [149, 2, 3], [149, 3, 2], [151, 2, 2], [151, 2, 3], [151, 3, 2], [157, 2, 2], [157, 2, 3], [157, 3, 2], [163, 2, 2], [163, 2, 3], [163, 3, 2], [167, 2, 2], [173, 2, 2], [179, 2, 2], [181, 2, 2], [191, 2, 2], [193, 2, 2], [197, 2, 2], [199, 2, 2], [211, 2, 2], [223, 2, 2], [227, 2, 2], [229, 2, 2], [233, 2, 2], [239, 2, 2], [241, 2, 2]]

Flowchart:

Flowchart: Python - Find all integers that are the product of exactly three primes.

For more Practice: Solve these Related Problems:

  • Write a Python program to list all integers up to 1000 that are exactly the product of three prime numbers, and represent each as a list of factors.
  • Write a Python program to generate combinations of three primes that multiply to a value less than or equal to 1000.
  • Write a Python program to use a sieve to find prime numbers and then test every combination of three for their product.
  • Write a Python program to represent each qualifying integer as a list of its three prime factors, ensuring factors are ordered as they appear.

Go to:


Previous: Find an integer with the given number of even and odd digits.
Next: Each triple of eaten, need, stock return a pair of total appetite and remaining.

Python Code Editor :

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

What is the difficulty level of this exercise?

Test your Programming skills with w3resource's quiz.



Follow us on Facebook and Twitter for latest update.