Python combinations generator using generators
6. Combinations Generator
Write a Python program to implement a generator that yields all possible combinations of a given list of elements.
In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter (unlike permutations). For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S.
Sample Solution:
Python Code:
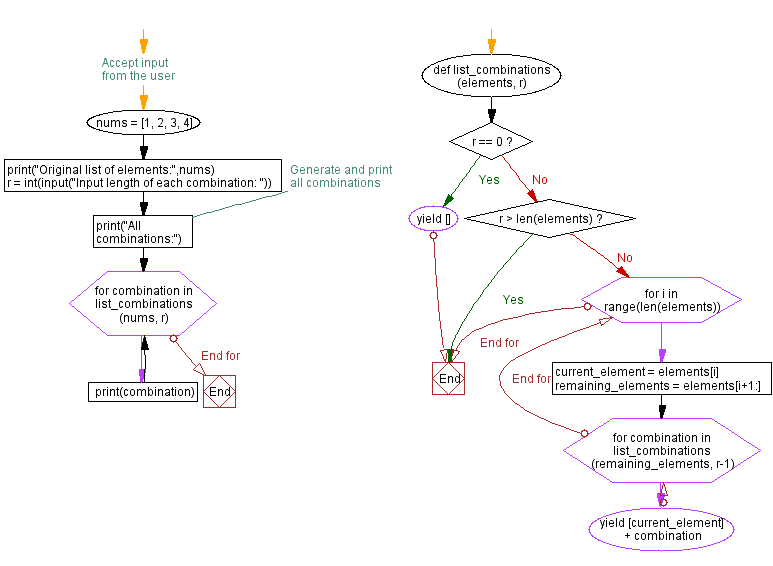
def list_combinations(elements, r):
if r == 0:
yield []
elif r > len(elements):
return
else:
for i in range(len(elements)):
current_element = elements[i]
remaining_elements = elements[i+1:]
for combination in list_combinations(remaining_elements, r-1):
yield [current_element] + combination
# Accept input from the user
nums = [1, 2, 3, 4]
print("Original list of elements:",nums)
r = int(input("Input length of each combination: "))
# Generate and print all combinations
print("All combinations:")
for combination in list_combinations(nums, r):
print(combination)
Sample Output:
Original list of elements: [1, 2, 3, 4] Input length of each combination: 3 All combinations: [1, 2, 3] [1, 2, 4] [1, 3, 4] [2, 3, 4]
Original list of elements: [1, 2, 3, 4] Input length of each combination: 4 All combinations: [1, 2, 3, 4]
Explanation:
In the above exercise,
- The combinations() function is defined as a generator function that takes two parameters: elements (the list of elements) and r (the length of each combination).
- If "r" is 0, it means we have generated a combination of lengths 0, so an empty list is yielded.
- If "r" is greater than the length of elements, it means the program cannot form combinations of lengths r from the given list, so the function returns.
- In the recursive case, the function iterates over the indices of the elements list using a for loop.
- Within the loop, the current element at index i is selected, and the remaining elements (elements[i+1:]) are stored in the remaining_elements variable.
- Another nested for loop is used to iterate over the combinations generated by recursively calling the combinations() function with the remaining_elements and r-1.
- For each combination, the current element is prepended to the combination using list concatenation ([current_element] + combination).
- The function yields each generated combination.
- The program accepts input from the user: "nums" represents the list of elements and "r" represents the length of each combination.
- The program prints a message indicating that it will generate all combinations.
- A for loop iterates over all combinations generated by the combinations() generator function.
- Inside the loop, each combination is printed using the print() function.
Flowchart:
For more Practice: Solve these Related Problems:
- Write a Python program to create a generator that yields all combinations of elements from a list for a given combination length r.
- Write a Python function that generates all non-repeating combinations of a list's elements and prints them in lexicographical order.
- Write a Python script to yield combinations of a list and then count and print the total number of combinations generated.
- Write a Python program to create a generator that produces all possible combinations (of any length) from a given list and outputs them as a nested list.
Go to:
Previous: Python permutations generator using generators.
Next: Python Collatz sequence generator using generators.
Python Code Editor:
Contribute your code and comments through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
