Python Data Structures and Algorithms - Recursion: Calculate the geometric sum

Python Recursion: Exercise-9 with Solution

Write a Python program to calculate the geometric sum up to 'n' terms.
Note : In mathematics, a geometric series is a series with a constant ratio between successive terms.

Sample Solution:

Python Code:

# Define a function named geometric_sum that calculates the geometric sum up to 'n' terms
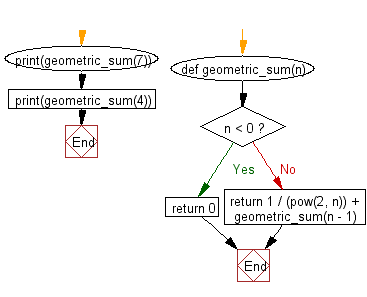
def geometric_sum(n):
    # Check if 'n' equals 0, which is the base case for the geometric sum
    if n == 0:  # Corrected base case condition
        # If 'n' equals 0, return 1 as the geometric sum in this case is 1
        return 1
    else:
        # If 'n' is not 0, calculate the term in the geometric series (1 / 2^n) and add it to
        # the result of recursively calling the geometric_sum function with 'n - 1'
        return 1 / (pow(2, n)) + geometric_sum(n - 1)
# Print the result of calling the geometric_sum function with the input value 7
print(geometric_sum(7))
# Print the result of calling the geometric_sum function with the input value 4
print(geometric_sum(4))

Sample Output:

1.9921875                                                                                                     
1.9375 

Flowchart:

Python Code Editor:

Contribute your code and comments through Disqus.

Previous: Write a Python program to calculate the harmonic sum of n-1.
Next: Write a Python program to calculate the value of 'a' to the power 'b'.