Python Challenges: Print a truth table for an infix logical expression

Python Challenges - 1: Exercise-56 with Solution

Write a Python program to print a truth table for an infix logical expression.

Sample Solution:

Python Code:

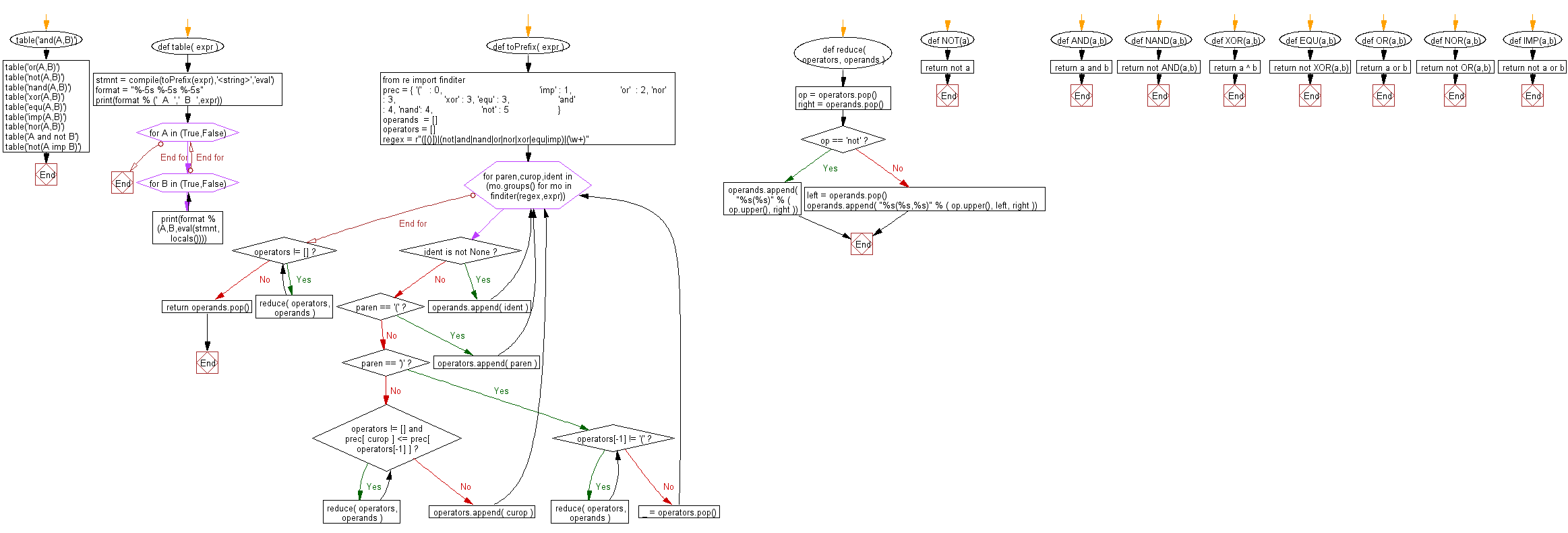
def table( expr ):
    """
     Ref.: https://bit.ly/3cWJD22
    table('A and not B')
      A     B   A and not B
    True  True  False
    True  False True
    False True  False
    False False False

    table('not(A imp B)')
      A     B   not(A imp B)
    True  True  False
    True  False True
    False True  False
    False False False
    """

    # convert infix expression to prefix (function call) form
    def toPrefix( expr ):
        from re import finditer

        # Pop and operator of the operators stack and one or two operands of the
        # operand stack, and assembled into a call to the appropriate function.
        # The function call is pushed onto the operand stack
        def reduce( operators, operands ):
            op = operators.pop()
            right = operands.pop()
            if op == 'not':
                operands.append( "%s(%s)" % ( op.upper(), right ))
            else:
                left = operands.pop()
                operands.append( "%s(%s,%s)" % ( op.upper(), left, right ))

        prec = { '('   : 0,                 # operator precedence
                 'imp' : 1,
                 'or'  : 2, 'nor' : 3,
                 'xor' : 3, 'equ' : 3,
                 'and' : 4, 'nand': 4,
                 'not' : 5
                 }

        # operand and operator stacks
        operands  = []
        operators = []

        # Regular expression for parsing the infix expression.  It has three
        # parenthesized groups, which are returned in a tuple by the groups()
        # method of a match object (mo).  The tuple is unpacked into
        # corresponding variables in the for-statement.
        #
        #         paren |    logical operators (curop)    |ident
        regex = r"([()])|(not|and|nand|or|nor|xor|equ|imp)|(\w+)"

        for paren,curop,ident in (mo.groups() for mo in finditer(regex,expr)):
            # identifiers (i.e., variable names) are pushed on the operand stack
            if ident is not None:
                operands.append( ident )

            # left parens are pushed on the operator stack
            elif paren == '(':
                operators.append( paren )

            # for a right paren, the stacks are reduced until the matching
            # left paren is encountered.  The left paren is discarded.
            elif paren == ')':
                while operators[-1] != '(':
                    reduce( operators, operands )

                _ = operators.pop()

            else:
                # while the operator being parsed (curop) has a lower
                # precedence than the one on the top of the operator stack,
                # reduce the higher priority operator.  Then push the curop
                # onto the operator stack
                while operators != [] and prec[ curop ] <= prec[ operators[-1] ]:
                    reduce( operators, operands )

                operators.append( curop )

        # after the input expression is exhausted, reduce the operands on the
        # operand stack until it is empty
        while operators != []:
            reduce( operators, operands )

        return operands.pop()

    def NOT(a): return not a
    def AND(a,b): return a and b
    def NAND(a,b): return not AND(a,b)
    def XOR(a,b): return a ^ b
    def EQU(a,b): return not XOR(a,b)
    def OR(a,b): return a or b
    def NOR(a,b): return not OR(a,b)
    def IMP(a,b): return not a or b

    stmnt = compile(toPrefix(expr),'','eval')

    format = "%-5s %-5s %-5s"
    print(format % ('  A  ','  B  ',expr))

    for A in (True,False):
        for B in (True,False):
            print(format % (A,B,eval(stmnt,locals())))

table('and(A,B)')
table('or(A,B)')
table('not(A,B)')
table('nand(A,B)')
table('xor(A,B)')
table('equ(A,B)')
table('imp(A,B)')
table('nor(A,B)')
table('A and not B')
table('not(A imp B)')

Sample Output:

  A     B   and(A,B)
True  True  True 
True  False False
False True  False
False False False
  A     B   or(A,B)
True  True  True 
True  False True 
False True  True 
False False False
  A     B   not(A,B)
True  True  False
True  False True 
False True  False
False False True 
  A     B   nand(A,B)
True  True  False
True  False True 
False True  True 
False False True 
  A     B   xor(A,B)
True  True  False
True  False True 
False True  True 
False False False
  A     B   equ(A,B)
True  True  True 
True  False False
False True  False
False False True 
  A     B   imp(A,B)
True  True  True 
True  False False
False True  True 
False False True 
  A     B   nor(A,B)
True  True  False
True  False False
False True  False
False False True 
  A     B   A and not B
True  True  False
True  False True 
False True  False
False False False
  A     B   not(A imp B)
True  True  False
True  False True 
False True  False
False False False

Flowchart:

Python Code Editor:

Contribute your code and comments through Disqus.

Previous: Write a Python program to compute the person's itinerary.
Next: Write a Python program to generate list with 'width'-bit gray code.