Python Challenges: Find the first triangle number to have over n divisors

Python Challenges - 1: Exercise-41 with Solution

Write a Python program to find the first triangle number to have over n(given) divisors.

From Wikipedia: A triangular number is a number that is the sum of all of the natural numbers up to a certain number. For example, 10 is a triangular number because 1 + 2 + 3 + 4 = 10. The first 25 triangular numbers are: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, and 351.
A triangular number is calculated by the equation: n(n+1)/2
The factors of the first five triangle numbers:
1: 1
3: 1, 3
6: 1, 2, 3, 6
10: 1, 2, 5, 10
15: 1, 3, 5, 15
In the above list 6 is the first triangle number to have over four divisors.

Sample Solution:

Python Code:

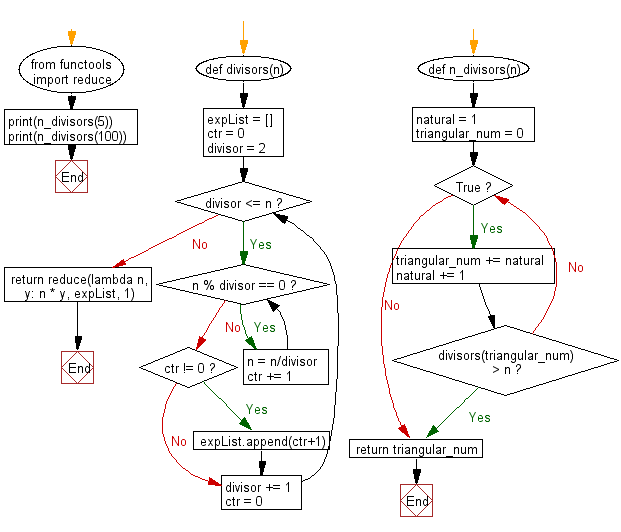
from functools import reduce
def divisors(n):
    expList = []
    ctr = 0
    divisor = 2
    while divisor <= n:
        while n % divisor == 0:
            n = n/divisor
            ctr += 1
        if ctr != 0:
            expList.append(ctr+1)
        divisor += 1
        ctr = 0
    return reduce(lambda n, y: n * y, expList, 1)


def n_divisors(n):
    natural = 1
    triangular_num = 0

    while True:
        triangular_num += natural
        natural += 1
        if divisors(triangular_num) > n:
            break
    return triangular_num

print(n_divisors(5))
print(n_divisors(100))

Sample Output:

28
73920

Flowchart:

Python Code Editor:

Contribute your code and comments through Disqus.

Previous: Write a Python program to find the product xyz.

Next: Write a Python program to find the starting number, under ten thousand will create the longest chain.