Python: Calculate Euclid's totient function of a given integer

Last update on April 17 2025 13:00:55 (UTC/GMT +8 hours)

Euclid's Totient Function

In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as φ(n) or ϕ(n), and may also be called Euler's phi function.
Write a Python program to calculate Euclid's totient function for a given integer. Use a primitive method to calculate Euclid's totient function.

Sample Solution:

Python Code:

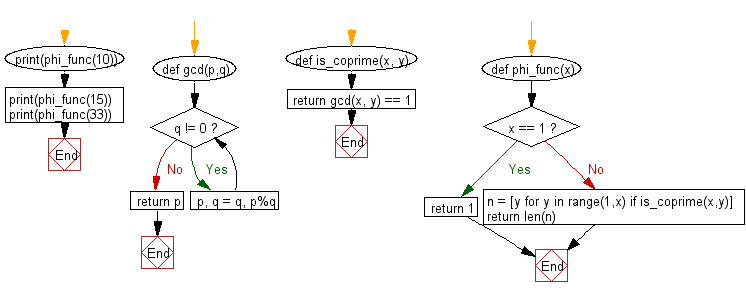
# Define a function 'gcd' to calculate the greatest common divisor (GCD) of two positive integers.
def gcd(p, q):
    # Use Euclid's algorithm to find the GCD.
    while q != 0:
        p, q = q, p % q
    return p

# Define a function 'is_coprime' to check if two numbers are coprime (GCD is 1).
def is_coprime(x, y):
    # Check if the GCD of 'x' and 'y' is equal to 1.
    return gcd(x, y) == 1

# Define a function 'phi_func' to calculate Euler's totient function for a given number 'x'.
def phi_func(x):
    # If 'x' is 1, return 1 since there is only one positive integer less than 1.
    if x == 1:
        return 1
    else:
        # Use list comprehension to find numbers less than 'x' that are coprime to 'x'.
        n = [y for y in range(1, x) if is_coprime(x, y)]
        # Return the count of coprime numbers, which is Euler's totient function value.
        return len(n)

# Test cases to calculate Euler's totient function for different numbers.
print(phi_func(10))
print(phi_func(15))
print(phi_func(33))

Sample Output:

4
8
20

Explanation:

Here is a breakdown of the above Python code:

GCD Calculation (gcd function):

The "gcd()" function uses Euclid's algorithm to calculate the greatest common divisor of two positive integers ('p' and 'q').

Coprime check (is_coprime function):

The "is_coprime()" function checks if two numbers ('x' and 'y') are coprime by comparing their GCD with 1.

Euler's Totient function (phi_func function):

The "phi_func()" function calculates Euler's totient function for a given number ('x') by finding the count of numbers less than 'x' that are coprime to 'x'.

Flowchart:

For more Practice: Solve these Related Problems:

Write a Python program to calculate Euler's totient function for a given integer by counting numbers coprime to it.
Write a Python program to compute the totient of a number using a naive iterative approach over possible divisors.
Write a Python program to implement Euler's totient function using a loop and the math.gcd function.
Write a Python program to compute the totient value of an integer by checking each number's co-primality with it.

Go to:

Previous: Write a Python program to check if two given numbers are Co Prime or not. Return True if two numbers are Co Prime otherwise return false.
Next: Write a Python program to create a coded string from a given string, using specified formula.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.