PHP Exercises: Print the number of combinations

Last update on April 19 2025 11:50:28 (UTC/GMT +8 hours)

66. Goldbach Partition Count

Write a PHP program that accept an even number (n should be greater than or equal to 4 and less than or equal to 50000, Goldbach number) from the user and create a combinations that express the given number as a sum of two prime numbers. Print the number of combinations.
Goldbach number: A Goldbach number is a positive even integer that can be expressed as the sum of two odd primes.[4] Since four is the only even number greater than two that requires the even prime 2 in order to be written as the sum of two primes, another form of the statement of Goldbach's conjecture is that all even integers greater than 4 are Goldbach numbers.
The expression of a given even number as a sum of two primes is called a Goldbach partition of that number. The following are examples of Goldbach partitions for some even numbers:
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 = 5 + 5
12 = 7 + 5
...
100 = 3 + 97 = 11 + 89 = 17 + 83 = 29 + 71 = 41 + 59 = 47 + 53.

Input: n ( n ≤ 10000). Input 0 to exit the program.

Sample Solution:

PHP Code:

<?php
// Define constants for maximum value and count
define('MAX', 50001);
define('COUNT', 5133);

// Create a fixed-size array for the prime table
$table = new SplFixedArray(MAX);
$table[0] = $table[1] = false;

// Create a fixed-size array to store prime numbers
$primes = new SplFixedArray(COUNT);
$p_i = 0;
$i = 2;

// Sieve of Eratosthenes algorithm to find prime numbers up to MAX
while ($i < MAX) {
    $primes[$p_i++] = $i;
    $table[$i] = true;

    // Mark multiples of the current prime as non-prime
    for ($j = $i * 2; $j < MAX; $j += $i) {
        $table[$j] = false;
    }

    // Move to the next prime
    while (++$i < MAX && $table[$i] === false);
}

// Process input until '0' is entered
while (true) {
    // Read an integer from the standard input
    fscanf(STDIN, '%d', $n);

    // Break the loop if '0' is entered
    if ($n === 0) {
        break;
    }

    // Initialize a counter for combinations
    $c = 0;

    // Check combinations of primes up to n/2
    for ($i = 0; $i < COUNT; $i++) {
        // Break if the prime is greater than n/2
        if ($primes[$i] > $n / 2) {
            break;
        }

        // Check if the complement is also a prime
        if ($table[$n - $primes[$i]]) {
            $c++;
        }
    }

    // Output the result
    echo "Number of combinations: ";
    echo $c . PHP_EOL;
}

?>

Explanation:

Define Constants:

Two constants are defined: MAX set to 50001 (the upper limit for prime number generation) and COUNT set to 5133 (the number of prime numbers expected within that limit).

Create Prime Table Array:

A fixed-size array $table is created using SplFixedArray to store boolean values indicating whether each number is prime. The first two indices, 0 and 1, are set to false (not prime).

Create Primes Array:

Another fixed-size array $primes is created to store the actual prime numbers found, and a variable $p_i is initialized to track the index for the primes array.

Sieve of Eratosthenes Algorithm:

The algorithm starts with i set to 2 and marks it as prime by storing it in the $primes array and setting $table[$i] to true.
A nested for loop marks all multiples of i (starting from 2i) as non-prime by setting corresponding indices in $table to false.
The outer loop continues, moving to the next unmarked number, indicating the next prime.

Input Processing Loop:

A while (true) loop is used to continuously read input from standard input until a 0 is entered.
Each input number is read and stored in the variable $n.

Check for Prime Combinations:

A counter $c is initialized to count valid combinations.
A for loop iterates through the prime numbers stored in $primes up to n/2.
For each prime, it checks if its complement (i.e., n - prime) is also prime using the $table array.
If the complement is prime, the counter $c is incremented.

Output the Result:

After checking all combinations for a given n, the code outputs the total number of valid combinations where the two primes sum up to n.

Sample Input:
100
0

Sample Output:

Number of combinations: 6

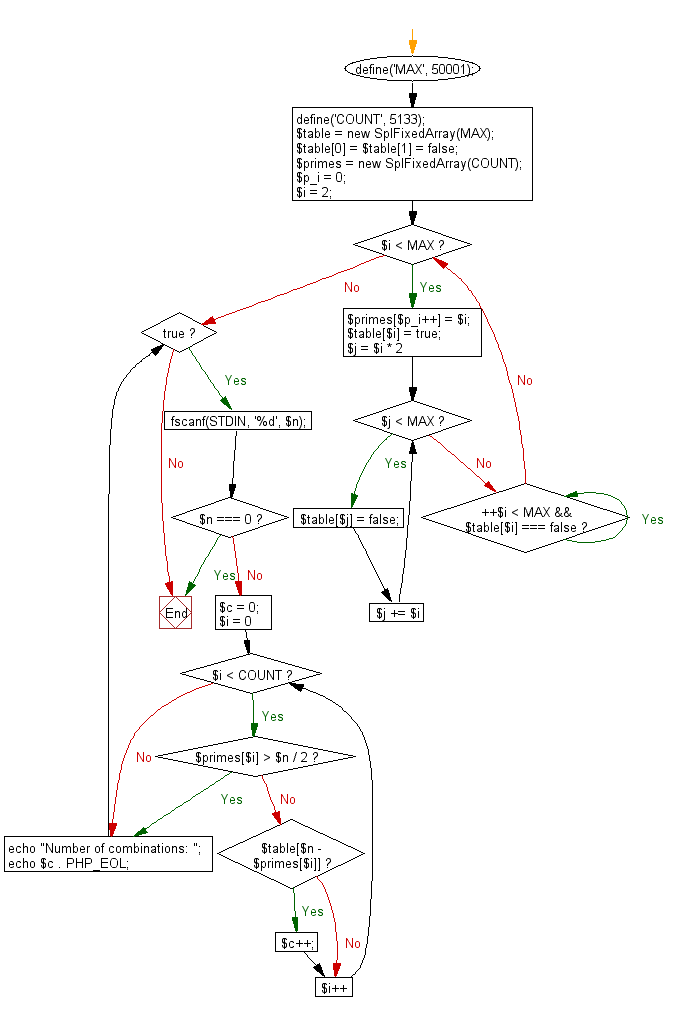
Flowchart:

For more Practice: Solve these Related Problems:

Write a PHP script to find all pairs of prime numbers that add up to a given even number and count them.
Write a PHP function to generate a list of prime numbers and determine the number of Goldbach partitions for an even integer.
Write a PHP script to compute and display every valid pair of primes that sum to the target even number.
Write a PHP script to use sieve methods and combination logic to count Goldbach partitions for given inputs.

PHP Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

Previous: Write a PHP program to compute the sum of first n given prime numbers.
Next: Write a PHP program to create maximum number of regions obtained by drawing n given straight lines.