NumPy np.exp: Usage, Applications, and Performance
Mastering NumPy’s np.exp: Exponential Functions in Python
Introduction to NumPy and np.exp
NumPy is a foundational Python library for numerical computing, enabling efficient array operations and mathematical functions. Among its tools, np.exp stands out as a critical function for calculating the exponential value of elements in an array.
What is np.exp?
- Computes ex where e is Euler’s number (~2.71828).
- Operates element-wise on arrays, lists, or scalars.
Importance of np.exp
- Machine Learning: Powers activation functions like Sigmoid and Softmax.
- Scientific Computing: Models exponential growth/decay in physics and chemistry.
- Data Analysis: Used in probability distributions and financial modeling.
Mathematical Background of Exponential
The exponential function ex is defined as:
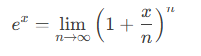
Key Properties
- Growth Rate: Rapidly increases for positive xx, decays for negative xx.
- Differentiation: d/dx ex=ex (unique among functions).
- Inverse: The natural logarithm (ln) reverses exponentiation: ln(ex) = x.
How np.exp works in NumPy
Element-Wise Operation
import numpy as np # Example 1: Apply np.exp to a scalar x = 2.0 result = np.exp(x) # Output: 7.389 (e^2) # Example 2: Apply np.exp to an array arr = np.array([1, 2, 3]) exp_arr = np.exp(arr) # Output: [2.718, 7.389, 20.085]
Input Types & Behavior
- Inputs: Integers, floats, arrays, or lists.
- Negative Values: Returns decay (e.g., e-1=0.368).
- Large Numbers: May cause overflow (e.g., e1000→∞).
Applications of np.exp
1. Machine Learning: Softmax Activation
import numpy as np
def softmax(scores):
# Step 1: Compute exponentials
exp_scores = np.exp(scores) # Converts scores to positive values
# Step 2: Normalize by sum of exponentials
return exp_scores / np.sum(exp_scores)
scores = np.array([2.0, 1.0, 0.1])
print(softmax(scores)) # Output: [0.659, 0.242, 0.099]
2. Statistics: Gaussian Distribution
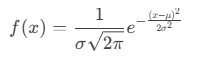
3. Finance: Compound Interest
import numpy as np principal = 1000 rate = 0.05 time = 10 # Continuous compounding: A = P * e^(rt) amount = principal * np.exp(rate * time) # Output: 1648.72
4. Physics: Radioactive Decay
N(t)=N0e−λt
Performance Considerations & Alternatives
Efficiency in NumPy
- Vectorization: Faster than Python loops (C-optimized backend).
- Broadcasting: Applies np.exp to multi-dimensional arrays seamlessly.
Precision Issues
- Overflow: np.exp(1000) returns inf (use np.clip for stability).
- Underflow: np.exp(-1000) returns 0 (use log-space operations).
Alternatives
- scipy.special.expit: Sigmoid function with numerical stability.
- np.expm1: Computes ex −1 accurately for small x.
Comparison with Other NumPy Functions
| Function | Use Case | Example |
|---|---|---|
| np.exp | Compute ex | np.exp(2) → 7.389 |
| np.power | Compute ab for any base aa | np.power(2, 3) → 8 |
| np.log | Compute natural logarithm (ln) | np.log(7.389) → 2.0 |
| np.expm1 | Compute ex−1 for small x | np.expm1(0.001) → 0.001001 (precise) |
Trends & Innovations
- GPU Acceleration: Libraries like CuPy leverage GPUs for faster np.exp computations.
- AI Applications: Optimized exponentiation for transformer models and neural networks.
- Precision Handling: New algorithms to reduce underflow/overflow in edge cases.
