Numpy.convolve in Python

Understanding Numpy.convolve: Perform Convolution on Arrays

np.convolve is a NumPy function that performs a discrete, linear convolution of two one-dimensional sequences. Convolution is widely used in signal processing, statistics, and machine learning for combining two sequences to create a third sequence that represents their interaction.

Syntax:

numpy.convolve(a, v, mode='full')

Parameters:

1. a (array_like): The first input sequence.

2. v (array_like): The second input sequence.

3. mode (str, optional): Determines the output length. Options:

• 'full' (default): Returns the complete convolution.
• 'valid': Returns only those parts of the convolution that are computed without padding.
• 'same': Returns an output array of the same length as a.

Returns:

An array containing the result of the convolution.

Examples and Code:

Example 1: Full Convolution

Code:

import numpy as np

# Define two input sequences
a = [1, 2, 3]
v = [0, 1, 0.5]

# Perform full convolution
result = np.convolve(a, v, mode='full')

# Print the result
print("Full convolution result:", result)

Output:

Full convolution result: [0.  1.  2.5 4.  1.5]

Explanation:

The full mode computes the complete convolution, including zero-padded edges.

Example 2: Same-Length Convolution

Code:

import numpy as np

# Define input sequences
a = [1, 2, 3, 4]
v = [0.2, 0.8]

# Perform same-length convolution
result = np.convolve(a, v, mode='same')

# Print the result
print("Same-length convolution result:", result)

Output:

Same-length convolution result: [0.2 1.2 2.2 3.2]

Explanation:
The same mode ensures that the output length matches the length of a.

Example 3: Valid Convolution

Code:

import numpy as np

# Define input sequences
a = [3, 4, 5, 6]
v = [1, -1]

# Perform valid convolution
result = np.convolve(a, v, mode='valid')

# Print the result
print("Valid convolution result:", result)

Output:

Valid convolution result: [1 1 1]

Explanation:
The valid mode excludes edge effects and computes only the convolution for positions where both sequences fully overlap.

Example 4: Application in Signal Processing

Code:

import numpy as np
import matplotlib.pyplot as plt

# Define a simple signal and a smoothing kernel
signal = [0, 1, 2, 1, 0, -1, -2, -1, 0]
kernel = [0.2, 0.5, 0.2]

# Perform convolution to smooth the signal
smoothed_signal = np.convolve(signal, kernel, mode='same')

# Plot the results
plt.plot(signal, label="Original Signal")
plt.plot(smoothed_signal, label="Smoothed Signal", linestyle="--")
plt.legend()
plt.show()

Output:

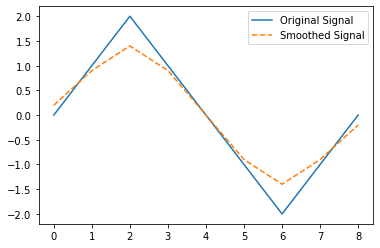
Explanation:
This example demonstrates how convolution can smooth a noisy signal using a smoothing kernel.

Key Notes:

1. Order of Inputs: While convolution is commutative for many cases, the order of a and v can affect padding in modes like 'same'.

2. Efficiency: np.convolve is optimized for 1D sequences. For multi-dimensional data, consider scipy.signal.convolve.

3. Applications:

• Image processing (e.g., blurring).
• Signal filtering and smoothing.
• Calculating moving averages in time-series analysis.

Additional Tips:

• For element-wise multiplication in the frequency domain (closely related to convolution), use Fourier Transform via np.fft.fft.
• If you need multi-dimensional convolution, explore scipy.signal.convolve2d.

Practical Guides to NumPy Snippets and Examples.