JavaScript: Calculate the extended Euclid Algorithm or extended GCD

JavaScript Math: Exercise-47 with Solution

Extended Euclid Algorithm

Write a JavaScript function to calculate the extended Euclid Algorithm or extended GCD.

In mathematics, the Euclidean algorithm[a], or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two numbers, the largest number that divides both of them without leaving a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in Euclid's Elements. It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

Visual Presentation:

Sample Solution:

JavaScript Code:

// Define a function named Euclid_gcd that calculates the greatest common divisor (GCD) using Euclid's algorithm.
function Euclid_gcd(a, b) {
  // Convert 'a' and 'b' to numbers.
  a = +a;
  b = +b;
  // Check if 'a' or 'b' is NaN (Not a Number).
  if (a !== a || b !== b) {
    return [NaN, NaN, NaN];
  }
  
  // Check if 'a' or 'b' is Infinity or -Infinity.
  if (a === Infinity || a === -Infinity || b === Infinity || b === -Infinity) {
    return [Infinity, Infinity, Infinity];
  }
  
  // Check if 'a' or 'b' are decimals.
  if ((a % 1 !== 0) || (b % 1 !== 0)) {
    return false;
  }
  
  // Initialize variables for signs and quotient.
  var signX = (a < 0) ? -1 : 1,
    signY = (b < 0) ? -1 : 1,
    x = 0,
    y = 1,
    u = 1,
    v = 0,
    q, r, m, n;
  
  // Get the absolute values of 'a' and 'b'.
  a = Math.abs(a);
  b = Math.abs(b);

  // Implement Euclid's algorithm to find the GCD.
  while (a !== 0) {
    q = Math.floor(b / a);
    r = b % a;
    m = x - u * q;
    n = y - v * q;
    b = a;
    a = r;
    x = u;
    y = v;
    u = m;
    v = n;
  }
  
  // Return an array containing the GCD, and the coefficients for 'a' and 'b'.
  return [b, signX * x, signY * y];
}

// Output the result of Euclid's algorithm for GCD calculation with inputs 17 and 4.
console.log(Euclid_gcd(17, 4));

Output:

[1,1,-4]

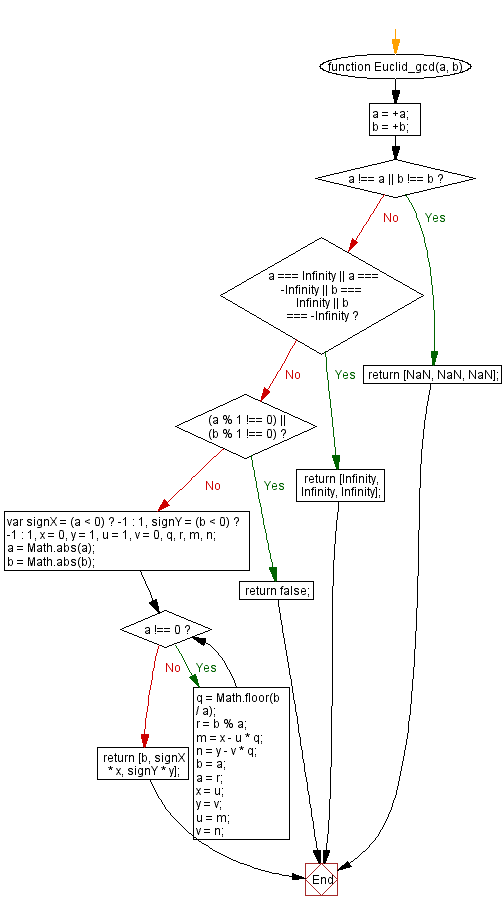
Flowchart:

Live Demo:

See the Pen javascript-math-exercise-47 by w3resource (@w3resource) on CodePen.

For more Practice: Solve these Related Problems:

• Write a JavaScript function that implements the Extended Euclidean Algorithm to compute the GCD and the Bezout coefficients.
• Write a JavaScript function that recursively calculates the extended GCD and returns an object with the coefficients.
• Write a JavaScript function that uses iteration to perform the Extended Euclid Algorithm and logs each computation step.
• Write a JavaScript function that validates input numbers and computes the extended GCD for cryptographic applications.

Go to:

• JavaScript Math and Numbers Exercises Home ↩
• JavaScript Exercises Home ↩

PREV : Calculate Divisor and Modulus.
NEXT : Calculate Falling Factorial.

Improve this sample solution and post your code through Disqus.