Java: Heap sort Algorithm
5. Heap Sort Implementation
Write a Java program to sort an array of given integers using the Heap sort algorithm.
In computer science heapsort (invented by J. W. J. Williams in 1964) is a comparison-based sorting algorithm. Heapsort can be thought of as an improved selection sort: like that algorithm, it divides its input into a sorted and an unsorted region, and it interactively shrinks the unsorted region by extracting the largest element and moving that to the sorted region. The improvement consists of the use of a heap data structure rather than a linear-time search to find the maximum. Although somewhat slower in practice on most machines than a well-implemented quicksort, it has the advantage of a more favorable worst-case O(n log n) runtime. Heapsort is an in-place algorithm, but not a stable sort.
A run of the heapsort algorithm sorting an array of randomly permuted values. In the first stage of the algorithm the array elements are reordered to satisfy the heap property. Before the actual sorting takes place, the heap tree structure is shown briefly for illustration.
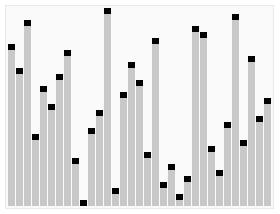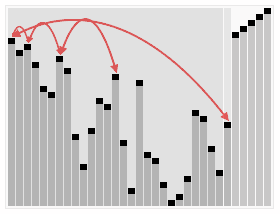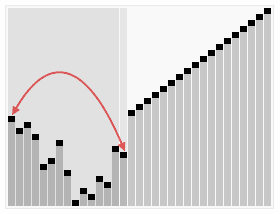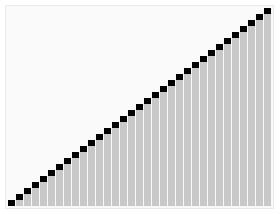
Animation credits : RolandH
Pseudocode:
// Ref.: https://bit.ly/2DBQsFI
function heapSort(a, count) is
input: an unordered array a of length count
(first place a in max-heap order)
heapify(a, count)
end := count - 1
while end > 0 do
(swap the root(maximum value) of the heap with the
last element of the heap)
swap(a[end], a[0])
(decrement the size of the heap so that the previous
max value will stay in its proper place)
end := end - 1
(put the heap back in max-heap order)
siftDown(a, 0, end)
function heapify(a,count) is
(start is assigned the index in a of the last parent node)
start := (count - 2) / 2
while start ≥ 0 do
(sift down the node at index start to the proper place
such that all nodes below the start index are in heap
order)
siftDown(a, start, count-1)
start := start - 1
(after sifting down the root all nodes/elements are in heap order)
function siftDown(a, start, end) is
(end represents the limit of how far down the heap to sift)
root := start
while root * 2 + 1 ≤ end do (While the root has at least one child)
child := root * 2 + 1 (root*2+1 points to the left child)
(If the child has a sibling and the child's value is less than its sibling's...)
if child + 1 ≤ end and a[child] < a[child + 1] then
child := child + 1 (... then point to the right child instead)
if a[root] < a[child] then (out of max-heap order)
swap(a[root], a[child])
root := child (repeat to continue sifting down the child now)
else
return
Sample Solution:
Java Code:
public class HeapSort
{
public static void heapSort(int[] a){
int count = a.length;
//first place a in max-heap order
heapify(a, count);
int end = count - 1;
while(end > 0){
//swap the root(maximum value) of the heap with the
//last element of the heap
int tmp = a[end];
a[end] = a[0];
a[0] = tmp;
//put the heap back in max-heap order
siftDown(a, 0, end - 1);
//decrement the size of the heap so that the previous
//max value will stay in its proper place
end--;
}
}
public static void heapify(int[] a, int count){
//start is assigned the index in a of the last parent node
int start = (count - 2) / 2; //binary heap
while(start >= 0){
//sift down the node at index start to the proper place
//such that all nodes below the start index are in heap
//order
siftDown(a, start, count - 1);
start--;
}
//after sifting down the root all nodes/elements are in heap order
}
public static void siftDown(int[] a, int start, int end){
//end represents the limit of how far down the heap to sift
int root = start;
while((root * 2 + 1) <= end){ //While the root has at least one child
int child = root * 2 + 1; //root*2+1 points to the left child
//if the child has a sibling and the child's value is less than its sibling's...
if(child + 1 <= end && a[child] < a[child + 1])
child = child + 1; //... then point to the right child instead
if(a[root] < a[child]){ //out of max-heap order
int tmp = a[root];
a[root] = a[child];
a[child] = tmp;
root = child; //repeat to continue sifting down the child now
}else
return;
}
}
// Driver program
public static void main(String args[])
{
int arr[] = {7, -5, 3, 2, 1, 0, 45};
int n = arr.length;
HeapSort ob = new HeapSort();
ob.heapSort(arr);
System.out.println("Sorted array:");
for (int element: arr) {
System.out.print(" "+element);
}
}
}
Sample Output:
Sorted array: -5 0 1 2 3 7 45
Flowchart:
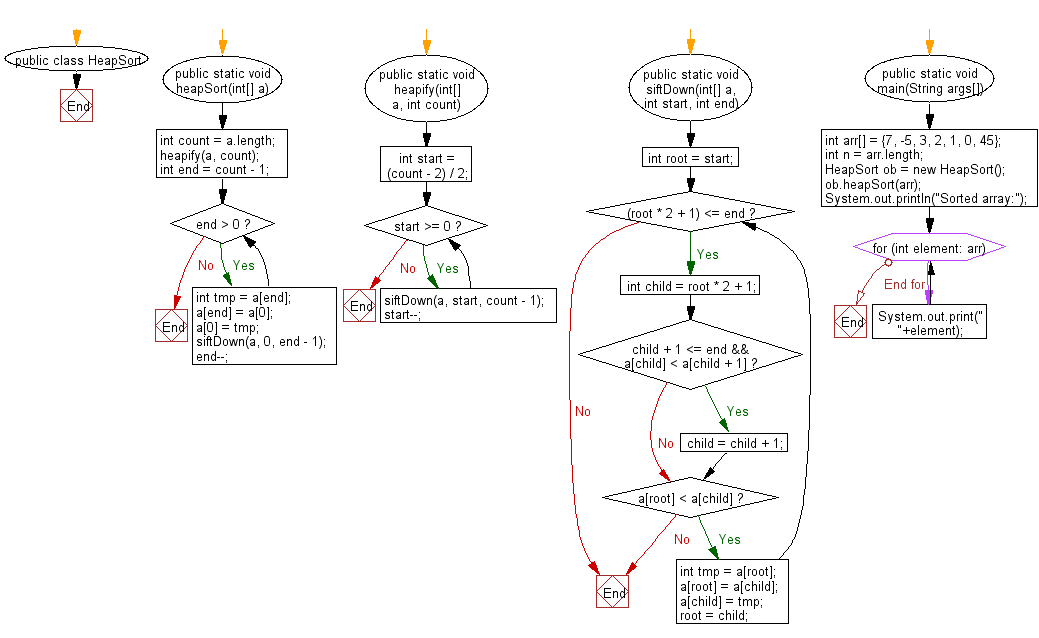
For more Practice: Solve these Related Problems:
- Write a Java program to implement heap sort and build the heap in O(n) time from an unsorted array.
- Write a Java program to modify heap sort to sort an array of objects based on a specified attribute.
- Write a Java program to implement heap sort in descending order by adjusting the heap condition.
- Write a Java program to implement a min-heap sort variation that sorts the array in ascending order using a min-heap.
Go to:
PREV : Merge Sort Implementation.
NEXT : Selection Sort Implementation.
Java Code Editor:
Contribute your code and comments through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
