Java: Find any number between 1 and n that can be expressed as the sum of two cubes in two (or more) different ways
Ramanujan Numbers
Write a Java program to find any number between 1 and n that can be expressed as the sum of two cubes in two (or more) different ways.
//http://introcs.cs.princeton.edu/java/13flow/Ramanujan.java.html
Here are some examples of Ramanujan numbers :
1729 = 1^3 + 12^3 = 9^3 + 10^3
* 10000
1729 = 1^3 + 12^3 = 9^3 + 10^3
4104 = 2^3 + 16^3 = 9^3 + 15^3
* 100000
1729 = 1^3 + 12^3 = 9^3 + 10^3
4104 = 2^3 + 16^3 = 9^3 + 15^3
13832 = 2^3 + 24^3 = 18^3 + 20^3
39312 = 2^3 + 34^3 = 15^3 + 33^3
46683 = 3^3 + 36^3 = 27^3 + 30^3
32832 = 4^3 + 32^3 = 18^3 + 30^3
40033 = 9^3 + 34^3 = 16^3 + 33^3
20683 = 10^3 + 27^3 = 19^3 + 24^3
65728 = 12^3 + 40^3 = 31^3 + 33^3
64232 = 17^3 + 39^3 = 26^3 + 36^3
Sample Solution:
Java Code:
import java.util.Scanner;
public class Example21 {
public static void main(String[] args) {
int n = 100000;
// for each a, b, c, d, check whether a^3 + b^3 = c^3 + d^3
for (int a = 1; a <= n; a++) {
int a3 = a*a*a;
if (a3 > n) break;
for (int b = a; b <= n; b++) {
int b3 = b*b*b;
if (a3 + b3 > n) break;
for (int c = a + 1; c <= n; c++) {
int c3 = c*c*c;
if (c3 > a3 + b3) break;
for (int d = c; d <= n; d++) {
int d3 = d*d*d;
if (c3 + d3 > a3 + b3) break;
if (c3 + d3 == a3 + b3) {
System.out.print((a3+b3) + " = ");
System.out.print(a + "^3 + " + b + "^3 = ");
System.out.print(c + "^3 + " + d + "^3");
System.out.println();
}
}
}
}
}
}
}
Sample Output:
1729 = 1^3 + 12^3 = 9^3 + 10^3 4104 = 2^3 + 16^3 = 9^3 + 15^3 13832 = 2^3 + 24^3 = 18^3 + 20^3 39312 = 2^3 + 34^3 = 15^3 + 33^3 46683 = 3^3 + 36^3 = 27^3 + 30^3 32832 = 4^3 + 32^3 = 18^3 + 30^3 40033 = 9^3 + 34^3 = 16^3 + 33^3 20683 = 10^3 + 27^3 = 19^3 + 24^3 65728 = 12^3 + 40^3 = 31^3 + 33^3 64232 = 17^3 + 39^3 = 26^3 + 36^3
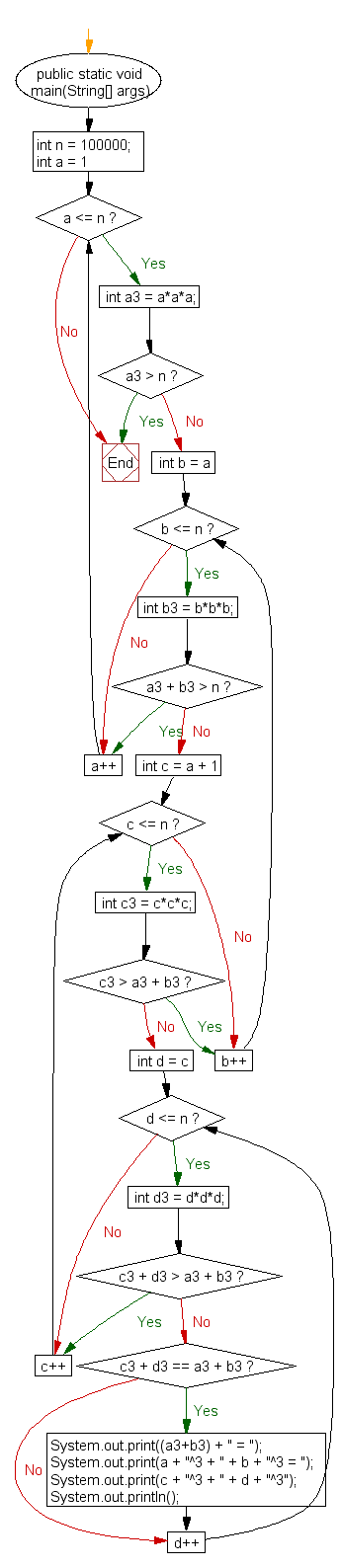
Flowchart:
For more Practice: Solve these Related Problems:
- Write a Java program to find numbers in a given range that can be expressed as the sum of two cubes in two distinct ways.
- Write a Java program to verify Ramanujan numbers by computing all possible pairs of cube sums for each number.
- Write a Java program to optimize the search for Ramanujan numbers using precomputed cube values.
- Write a Java program to generate and display Ramanujan numbers along with the cube pairs that form them.
Go to:
PREV : First 10 Fermat Numbers.
NEXT : Check Mersenne Number.
Java Code Editor:
Contribute your code and comments through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
