Java: Find the median of the number inside the window

Last update on May 14 2025 12:59:32 (UTC/GMT +8 hours)

Median in Sliding Window

Write a Java program to find the median of the numbers inside the window (size k) at each step in a given array of integers with duplicate numbers. Move the window to the array start.

{|1, 2, 3|, 4, 5, 6, 7, 8, 8} -> Return median 2
{1, |2, 3, 4|, 5, 6, 7, 8, 8} -> Return median 3
{1, 2, |3, 4, 5|, 6, 7, 8, 8} -> Return median 4
{1, 2, 3, |4, 5, 6|, 7, 8, 8} -> Return median 5
{1, 2, 3, 4, |5, 6, 7|, 8, 8} -> Return median 6
{1, 2, 3, 4, 5, |6, 7, 8|, 8} -> Return median 7
{1, 2, 3, 4, 5, 6, |7, 8, 8|} -> Return median 8
Result array {2, 3, 4, 5, 6, 7, 8}

Sample Solution:

Java Code:

// Importing necessary Java utilities
import java.util.*;
import java.util.Arrays;
import java.util.LinkedList;

// Defining a class named Solution
public class Solution {
  
  // The main method of the program
  public static void main(String[] args) {
    // Initializing an array and window size 'k'
    int[] main_array = {1, 2, 3, 4, 5, 6, 7, 8, 8};
    int k = 3;
    
    // Displaying the original array and value of 'k'
    System.out.println("\nOriginal array: " + Arrays.toString(main_array));
    System.out.println("\nValue of k: " + k);
    System.out.println("\nResult: ");
    
    // Getting the result of the median sliding window operation
    ArrayList<Integer> result = median_slide_window(main_array, k);
    
    // Displaying the result
    for (int i = 0; i < result.size(); i++) {
      System.out.println(result.get(i));
    }
  }
  
  // Method to compute the median in a sliding window of size 'k'
  public static ArrayList<Integer> median_slide_window(int[] main_array, int k) {
    ArrayList<Integer> result = new ArrayList<>();
    
    // If 'k' is 0 or greater than the length of the array, return an empty result
    if (k == 0 || main_array.length < k) {
      return result;
    }
    
    // PriorityQueues to store elements on the right and left side of the window
    PriorityQueue<Integer> right_num = new PriorityQueue<>(k);
    PriorityQueue<Integer> left_num = new PriorityQueue<>(k, Collections.reverseOrder());

    // Adding elements to the queues for initial window
    for (int i = 0; i < k - 1; ++i) {
      add(right_num, left_num, main_array[i]);
    }

    // Sliding the window and computing median
    for (int i = k - 1; i < main_array.length; ++i) {
      add(right_num, left_num, main_array[i]);
      int median = compute_median(right_num, left_num);
      result.add(median);
      remove(right_num, left_num, main_array[i - k + 1]);
    }
    
    return result; // Returning the result containing medians of the sliding window
  }

  // Method to compute the median from the PriorityQueues
  private static int compute_median(PriorityQueue<Integer> right_num, PriorityQueue<Integer> left_num) {
    if (left_num.isEmpty() && right_num.isEmpty()) {
      return 0; // Return 0 if both queues are empty
    }
    
    // Balancing the queues to get the median
    while (left_num.size() < right_num.size()) {
      left_num.add(right_num.poll());
    }

    while (left_num.size() - right_num.size() > 1) {
      right_num.add(left_num.poll());
    }
    
    return left_num.peek(); // Returning the median element
  }

  // Method to add elements to the PriorityQueues maintaining the order
  private static void add(PriorityQueue<Integer> right_num, PriorityQueue<Integer> left_num, int num) {
    if (left_num.isEmpty() && right_num.isEmpty()) {
      left_num.add(num);
      return;
    } else {
      if (num <= compute_median(right_num, left_num)) {
        left_num.add(num);
      } else {
        right_num.add(num);
      }
    }
  }

  // Method to remove elements from the PriorityQueues
  private static void remove(PriorityQueue<Integer> right_num, PriorityQueue<Integer> left_num, int num) {
    if (num <= compute_median(right_num, left_num)) {
      left_num.remove(num);
    } else {
      right_num.remove(num);
    }
  }
}

Sample Output:

Original array: [1, 2, 3, 4, 5, 6, 7, 8, 8]

Value of k: 3

Result: 
2
3
4
5
6
7
8

Pictorial Presentation:

Java exercises: Find the median of the number inside the window

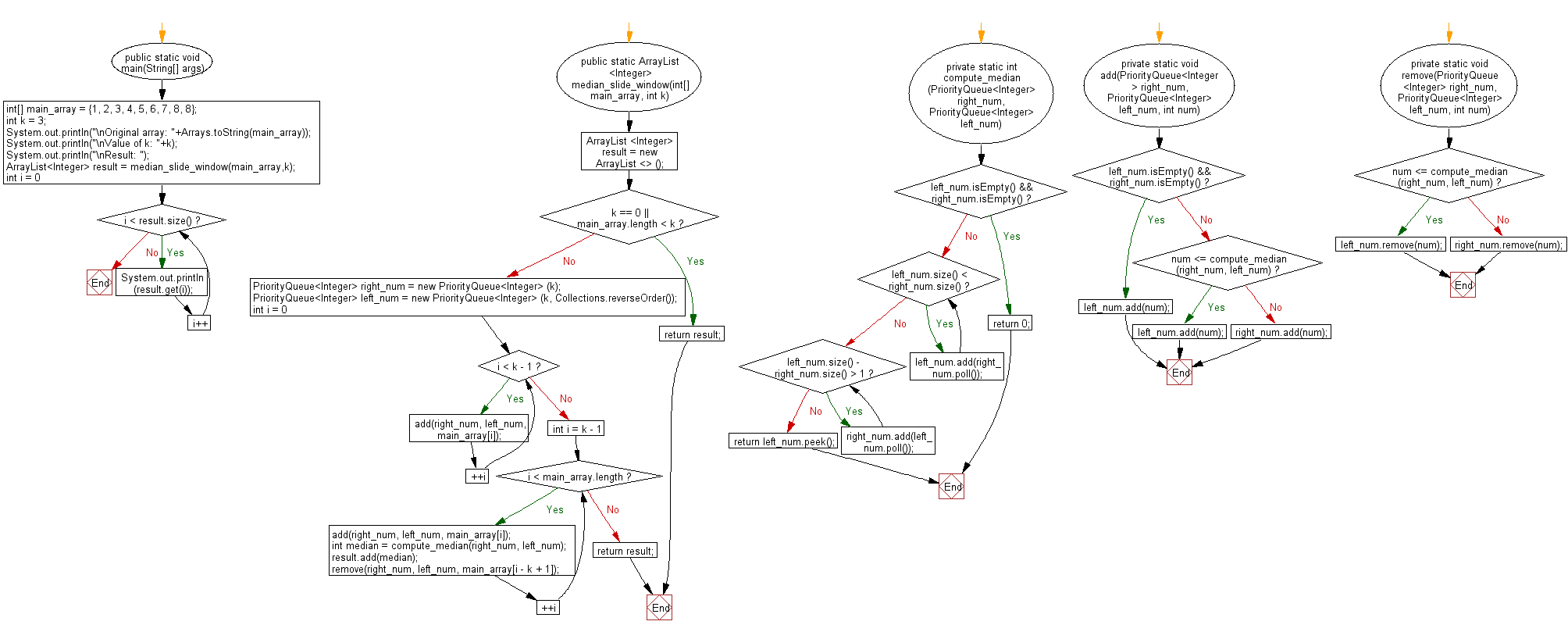
Flowchart:

For more Practice: Solve these Related Problems:

Write a Java program to compute the average of numbers in each sliding window of a given size in an array.
Write a Java program to calculate the sum of elements in every sliding window of size k in an array.
Write a Java program to determine the mode (most frequent element) within each sliding window of an array.
Write a Java program to find the minimum element in each sliding window of a given array.

Go to:

PREV : Elements Smaller Than Another Array.
NEXT : Max in Sliding Window.

Java Code Editor:

Company: Google

Contribute your code and comments through Disqus.