Efficient Solutions for Array Rotation

Rotate Array

Rotate an array to the right by k steps.

The "Rotate Array" problem involves rotating an array to the right by k steps. Given an array and an integer k, the goal is to shift the array elements to the right by k positions. The rotation should be cyclic, meaning the last k elements become the first k elements.

• Input and Output Requirements
• Real-world Scenario
• Underlying Concepts
• Examples and Illustrations
• Brute Force Approach
• Optimization Techniques
• Algorithmic Thinking
• Algorithmic Strategies
• Common Mistakes and Pitfalls
• Coding Best Practices
• Testing and Debugging
• Algorithm Analysis
• Application in Real-world Projects
• Example test cases
• Solution for different languages
• Time and Space Complexity

Input and Output Requirements:

• Input format:
• The input consists of an array of elements and an integer k.
• The array can contain integers, characters, or other data types.
• The value of k represents the number of steps to rotate the array.
• Output format:
• The output is the modified array after rotation.
• The modified array should have the same elements as the original array, but in rotated order.

Real-world Scenario:

Imagine a scenario where you have a list of tasks or events scheduled in an array, representing time slots. Rotating the array to the right by k steps simulates the passage of time, where tasks/events shift to later time slots. For instance,

Example:

• Original Schedule: [Task 1, Task 2, Task 3, Task 4, Task 5]
• After rotating by 2 steps: [Task 4, Task 5, Task 1, Task 2, Task 3]

Underlying Concepts:

Array Rotation:

• Introduction:
• Array rotation involves rearranging the elements of an array by shifting them to the right or left.
• Right Rotation:
• In the "Rotate Array" problem, right rotation refers to moving elements from the end to the beginning.
• Left Rotation (optional):
• While this problem focuses on right rotation, mention left rotation for a comprehensive understanding.

Modulo Operation:

• Handling Cyclic Rotations:
• Discuss how the modulo operation is utilized to handle cyclic rotations efficiently.
• When shifting elements to the right, using modulo helps to wrap around when reaching the end of the array.
• Modulo and Array Indices:
• Explain how taking the modulo of an index ensures that the rotation is cyclic and avoids index out-of-bounds errors.
• Example:
• If n is the length of the array and i is the current index, the new index after right rotation is (i + k) % n.
• Illustration:
• Use a visual aid or example to demonstrate how modulo ensures the cyclic property of the rotation.

Examples and Illustrations:

Walkthrough examples:

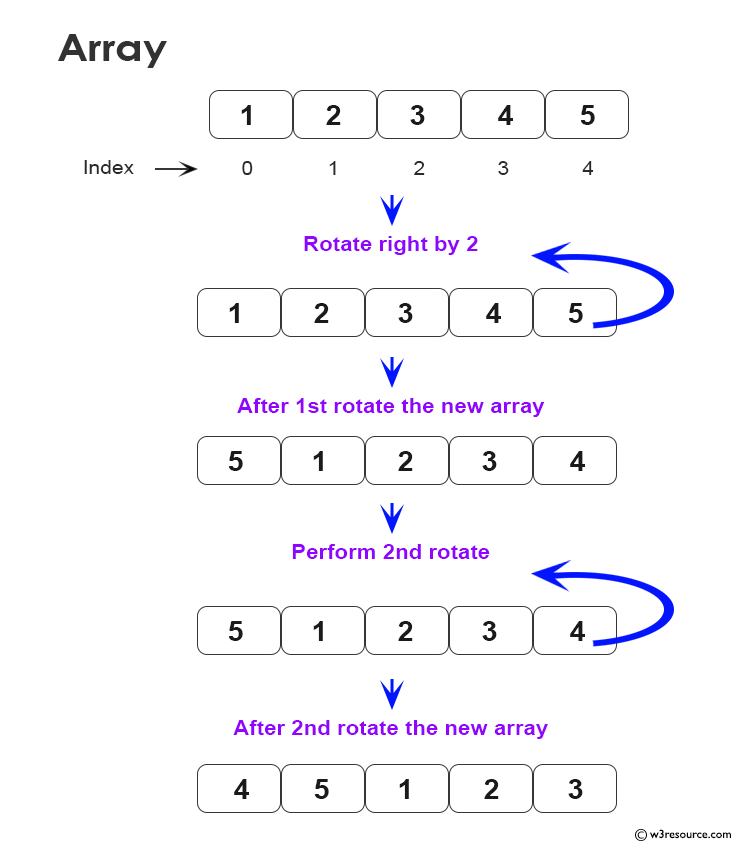
• Basic Example:
• Input Array: [1, 2, 3, 4, 5]
• Steps: Rotate right by 2
• Expected Output: [4, 5, 1, 2, 3]
• Manually demonstrate how each element moves to its new position.
• Negative Steps Example (optional):
• Input Array: [A, B, C, D, E]
• Steps: Rotate right by -1
• Expected Output: [E, A, B, C, D]
• Explain the concept of rotating in the opposite direction.

Visualization:

Brute Force Approach:

Naive Solution:

• Idea:
• One straightforward approach to rotate an array to the right by k steps is to repeatedly shift each element to its rightmost neighbor.
• Implementation steps:
• Repeat the process k times.
• For each rotation, iterate through the array from the end to the beginning.
• Shift each element one position to the right.

Pseudocode:

 procedure rotateArray(arr: array of elements, k: integer)
    n ← length(arr)
    k ← k % n   // Handle cases where k is greater than the length of the array
    reverseArray(arr, 0, n - 1)  // Reverse the entire array
    reverseArray(arr, 0, k - 1)  // Reverse the first k elements
    reverseArray(arr, k, n - 1)  // Reverse the remaining elements
end procedure
procedure reverseArray(arr: array of elements, start: integer, end: integer)
    while start < end do
        swap(arr[start], arr[end])
        start ← start + 1
        end ← end - 1
    end while
end procedure

The above pseudocode can be adapted for various programming languages such as Python, Java, C++, etc. The "reverseArray()" procedure is a generic helper function to reverse a portion of the array. The "rotateArray()" procedure uses this helper function to rotate the array by k steps. The modulo operation handles cases where k is greater than the length of the array.

Complexity Analysis:

• Time complexity:
• The outer loop runs k times, and for each rotation, the inner loop iterates through the entire array.
• Time Complexity: O(k * n), where n is the length of the array.
• Space complexity:
• The brute force approach modifies the array in-place, requiring constant extra space.
• Space Complexity: O(1).

Optimization Techniques:

Reversal Algorithm:

• Introduction:
• The reversal algorithm is an optimized approach for rotating an array to the right by k steps.
• Instead of shifting elements one by one, the algorithm performs three reversals to achieve the desired rotation.
• Steps:
• Reverse the entire array.
• Reverse the first k elements.
• Reverse the remaining elements.

Pseudocode:

procedure rotateReversal(nums: array of elements, k: integer)
    n ← length(nums)
    k ← k % n
    reverseArray(nums, 0, n - 1)
    reverseArray(nums, 0, k - 1)
    reverseArray(nums, k, n - 1)
end procedure

Complexity analysis:

• Time complexity:
• Three reversals take O(n) time, making the overall time complexity more efficient than the brute force approach.
• Space complexity:
• The algorithm performs the rotation in-place, using only constant extra space (O(1)).

Juggling algorithm (optional):

• Introduction (Optional):
• The juggling algorithm is an alternative approach to array rotation that uses the GCD (Greatest Common Divisor) of n and k.
• Steps (Optional):
• Find the GCD of n and k.
• Perform cyclic swaps based on the GCD.

Pseudocode (Optional):

procedure rotateJuggling(nums: array of elements, k: integer)
    n ← length(nums)
    k ← k % n
    gcd ← calculateGCD(n, k)

    for i ← 0 to gcd - 1 do
        temp ← nums[i]
        j ← i
        while true do
            d ← (j + k) % n
            if d = i then
                break
            end if
            nums[j] ← nums[d]
            j ← d
        end while
        nums[j] ← temp
    end for
end procedure

Complexity Analysis (Optional):

• The juggling algorithm has similar time complexity to the reversal algorithm, but involves more intricate calculations.
• Both time and space complexity are O(n).

Algorithmic Thinking:

Divide and Conquer:

• Breaking Down the Problem:
• Divide and Conquer involves breaking down a complex problem into simpler subproblems.
• For rotating an array, the initial complexity can be daunting, but breaking it into smaller steps makes it more manageable.
• Steps for Divide and Conquer:
• Identify key subproblems within the problem statement.
• Solve each subproblem independently.
• Combine the solutions of subproblems to obtain the overall solution.
• Application to "Rotate an Array":
• Identify the subproblems:
• Rotating a smaller segment of the array by k steps.
• Combining the rotations of smaller subsegments to achieve the final rotation.
• Effectiveness:
• Divide and Conquer is effective when the problem can be divided into smaller, more manageable parts.
• Each subproblem is solved independently, simplifying the overall problem-solving process.

Algorithmic Strategies:

• Introduction:
• Algorithmic strategies involve adopting specific techniques or approaches to tackle problems more efficiently.
• In the context of rotating an array, strategies like reversing segments and cyclic replacements are algorithmic approaches.
• Reversing Segments:
• Recognizing that rotating an array can be achieved by reversing segments of the array.
• This simplifies the problem, allowing for a more straightforward rotation.
• Cyclic replacements:
• Cyclic replacements offer a strategy for optimizing the solution by reducing the number of operations.
• Efficiently shift elements within the array to achieve the desired rotation.
• Algorithmic Efficiency:
• Algorithmic strategies aim to improve the efficiency of solving problems.
• Reversing segments and cyclic replacements provide alternative approaches that reduce time complexity.
• Adaptability:
• Algorithmic strategies adapt to various problem scenarios.
• They can be applied to different problems by leveraging the underlying principles.
• Problem-Specific Strategy:
• The choice of strategy depends on the problem requirements and constraints.
• Understanding the problem's nature guides the selection of the most appropriate strategy.

Common Mistakes and Pitfalls:

Handling Negative k:

• Issue:
• One common mistake is not handling negative values of k appropriately.
• Observations:
• If k is negative, it implies a left rotation instead of a right rotation.
• Ensure that the algorithm correctly handles negative values of k and performs the rotation in the intended direction.
• Example:
• If the array is [1, 2, 3, 4, 5] and k is -2, the correct result should be [3, 4, 5, 1, 2].

Array Size and k Relationship:

• Issue:
• Another potential mistake is not considering the relationship between the array size (n) and the value of k.
• Observations:
• If k is greater than the length of the array (k > n), the rotation becomes equivalent to rotating by k % n steps.
• Address scenarios where the array size is less than k and ensure a valid rotation.
• Example:
• If the array is [A, B, C] and k is 5, the rotation is equivalent to rotating by 2 steps (k % n), resulting in [B, C, A].

Coding Best Practices:

Modularity:

• Focus:
• Encourage the use of modular code by breaking down the rotation algorithm into well-defined functions or methods.
• Benefits:
• Modularity enhances code readability and maintainability.
• Each function or method should have a specific responsibility, making the code easier to understand.
• Example:

procedure rotateArray(nums: array of elements, k: integer)
    n ← length(nums)
    k ← k % n

    reverseArray(nums, 0, n - 1)
    reverseArray(nums, 0, k - 1)
    reverseArray(nums, k, n - 1)
end procedure

procedure reverseArray(nums: array of elements, start: integer, end: integer)
    // Implementation of array reversal
end procedure 

Variable Naming:

• Importance:
• Discuss the significance of using meaningful variable names to enhance code readability.
• Descriptive names:
• Choose variable names that reflect the purpose or role of the variable in the algorithm.
• Example:

procedure rotateArray(nums: array of elements, rotationSteps: integer)
    arrayLength ← length(nums)
    effectiveSteps ← rotationSteps % arrayLength

    reverseArray(nums, 0, arrayLength - 1)
    reverseArray(nums, 0, effectiveSteps - 1)
    reverseArray(nums, effectiveSteps, arrayLength - 1)
end procedure

procedure reverseArray(nums: array of elements, startIndex: integer, endIndex: integer)
    // Implementation of array reversal
end procedure

Testing and Debugging:

Test cases:

• Importance:
• Make sure that the array rotation algorithm is thoroughly tested to ensure its correctness.
• Test Case Selection:
• Provide a set of diverse test cases covering different scenarios:
• Positive values of 'k'.
• Negative values of 'k'.
• Edge cases (empty array, single-element array).
• Arrays with various data types (integers, characters, etc.).
• Example Test Cases:
• Original Array: [1, 2, 3, 4, 5], k = 2 Expected Result: [4, 5, 1, 2, 3]
• Original Array: ['A', 'B', 'C', 'D'], k = -1 Expected Result: ['D', 'A', 'B', 'C']
• Original Array: [] (empty array), k = 3 Expected Result: []
• Original Array: [10, 20, 30, 40, 50], k = 7 Expected Result: [40, 50, 10, 20, 30]

Debugging techniques:

• Common errors:
• Discuss common errors that might occur during array rotation and how to identify them:
• Incorrect handling of negative 'k' values.
• Incorrect modulo operation.
• Issues with array indexing.
• Debugging techniques:
• Encourage learners to use print statements or debugging tools to inspect variable values at different stages of the algorithm.
• Step through the algorithm manually for a small test case to identify any logical errors.
• Example Debugging Steps:
• Check the value of 'k' and ensure it is within a valid range.
• Verify the modulo operation's correctness for handling cyclic rotations.
• Inspect the array's intermediate state after each reversal operation.

Algorithm Analysis:

Time and Space Complexity:

• Time Complexity Analysis:
• Discuss the time complexity of the array rotation algorithm, considering the main operations performed.
• Analyze the time complexity of key components, such as array reversals and other relevant operations.
• For the reversal algorithm:
• Three reversals take O(n) time, where n is the length of the array.
• Space Complexity Analysis:
• Examine the space complexity of the algorithm by evaluating the amount of extra space required.
• For the reversal algorithm:
• The algorithm operates in-place, using only constant extra space (O(1)).
• Pseudocode:

procedure rotateReversal(nums: array of elements, k: integer)
    n ← length(nums)
    k ← k % n

    reverseArray(nums, 0, n - 1)
    reverseArray(nums, 0, k - 1)
    reverseArray(nums, k, n - 1)
end procedure

procedure reverseArray(nums: array of elements, start: integer, end: integer)
    // Implementation of array reversal
end procedure
 

Trade-offs:

• Time vs. Space Complexity Trade-off:
• Discuss any trade-offs between time and space complexity in the context of the array rotation algorithm.
• In the case of the reversal algorithm:
• Time complexity is optimized with O(n) time, but it uses constant extra space (O(1)).
• Comparison with Brute Force Approach:
• Compare the optimized algorithm with the brute force approach in terms of time and space complexity.
• Emphasize that the optimized algorithm provides a more efficient solution in terms of time complexity.

Application in Real-world Projects:

Practical Use Cases:

• Cyclic Scheduling:
• In scheduling applications, where tasks or events need to follow a cyclic pattern.
• For example, rotating a weekly schedule or managing recurring tasks.
• Data encryption:
• In certain encryption algorithms, where array rotation is used as a step in the encryption or decryption process.
• Rotation can introduce variability in the data, enhancing security.
• Image processing:
• In image processing, where rotating pixel values can be part of certain transformation operations.
• Useful for tasks such as rotating images or adjusting orientation.

Example test cases:

Positive cases with valid rotations:

• Input: nums = [1, 2, 3, 4, 5], k = 2
• Expected output: [4, 5, 1, 2, 3]
• Explanation: Rotate right by 2 steps, resulting in [4, 5, 1, 2, 3].
• Input: nums = [3, 2, 4], k = 1
• Expected output: [4, 3, 2]
• Explanation: Rotate right by 1 step, resulting in [4, 3, 2].

Negative cases with invalid rotations:

• Input: nums = [3, 5, 8, 2], k = 10
• Expected output: [8, 2, 3, 5]
• Explanation: Rotate right by 10 steps, which is equivalent to rotating by 2 steps as the array length is 4. The resulting array is [8, 2, 3, 5].
• Input: nums = [-1, -2, -3, -4, -5], k = 7
• Expected output: [-5, -1, -2, -3, -4]
• Explanation: Rotate right by 7 steps, which is equivalent to rotating by 2 steps as the array length is 5. Resulting array is [-5, -1, -2, -3, -4].

Edge cases with empty arrays, single-element arrays, and extreme values:

• Input: nums = [], k = 5
• Expected output: []
• Explanation: Empty array, no rotation possible.
• Input: nums = [5], k = 1
• Expected output: [5]
• Explanation: Single-element array, no rotation possible.
• Input: nums = [1000000000, -1000000000, 2000000000, -2000000000], k = 2
• Expected output: [2000000000, -2000000000, 1000000000, -1000000000]
• Explanation: Rotate right by 2 steps, resulting in [2000000000, -2000000000, 1000000000, -1000000000].

Solution for different languages:

Python - Rotate Array Solution:

Code:

def rotate_array(nums, k):
    # If k is greater than the length of nums, take its modulo
    k %= len(nums)
    # Reverse the entire array
    reverse(nums, 0, len(nums) - 1)
    # Reverse the first k elements
    reverse(nums, 0, k - 1)
    # Reverse the remaining elements
    reverse(nums, k, len(nums) - 1)
    return nums

def reverse(nums, start, end):
    # Helper function to reverse the array from start to end indices
    while start < end:
        nums[start], nums[end] = nums[end], nums[start]
        start += 1
        end -= 1

# Test cases
print(rotate_array([1, 2, 3, 4, 5], 2))  # Expected output: [4, 5, 1, 2, 3]
print(rotate_array([3, 2, 4], 1))        # Expected output: [4, 3, 2]
print(rotate_array([3, 5, 8, 2], 10))     # Expected output: [8, 2, 3, 5]
print(rotate_array([-1, -2, -3, -4, -5], 7))  # Expected output: [-4, -5, -1, -2, -3]

Output:

[4, 5, 1, 2, 3]
[4, 3, 2]
[8, 2, 3, 5]
[-4, -5, -1, -2, -3]

Explanation of the said Python code:

• The rotate_array function takes two parameters: 'nums', the array to be rotated, and 'k', the number of steps to rotate the array to the right.
• To handle cases where 'k' is greater than the length of 'nums', the function calculates 'k' modulo the length of 'nums'. This ensures that 'k' is within the range of the array length.
• The function then calls the "reverse()" function three times to rotate:
• First, it reverses the entire array using "reverse(nums, 0, len(nums) - 1)".
• Then, it reverses the first 'k' elements of the array using "reverse(nums, 0, k - 1)".
• Finally, it reverses the remaining elements of the array using "reverse(nums, k, len(nums) - 1)".
• The "reverse()" function reverses the elements of the array between the 'start' and 'end' indices.
• The function returns the rotated array 'nums' after reversals.

C++ - Rotate Array Solution:

Code:

#include <iostream>
#include <vector>
using namespace std;

void reverse(vector<int>& nums, int start, int end) {
    // Helper function to reverse the array from start to end indices
    while (start < end) {
        swap(nums[start], nums[end]);
        start++;
        end--;
    }
}

vector<int> rotateArray(vector<int>& nums, int k) {
    // If k is greater than the length of nums, take its modulo
    k %= nums.size();
    // Reverse the entire array
    reverse(nums, 0, nums.size() - 1);
    // Reverse the first k elements
    reverse(nums, 0, k - 1);
    // Reverse the remaining elements
    reverse(nums, k, nums.size() - 1);
    return nums;
}

int main() {
    // Create vectors explicitly
    vector<int> arr1 = {1, 2, 3, 4, 5};
    vector<int> result1 = rotateArray(arr1, 2);
    for (int num : result1) {
        cout << num << " ";
    }
    cout << endl; // Expected output: 4 5 1 2 3

    vector<int> arr2 = {3, 2, 4};
    vector<int> result2 = rotateArray(arr2, 1);
    for (int num : result2) {
        cout << num << " ";
    }
    cout << endl; // Expected output: 4 3 2

    vector<int> arr3 = {3, 5, 8, 2};
    vector<int> result3 = rotateArray(arr3, 10);
    for (int num : result3) {
        cout << num << " ";
    }
    cout << endl; // Expected output: 8 2 3 5

    vector<int> arr4 = {-1, -2, -3, -4, -5};
    vector<int> result4 = rotateArray(arr4, 7);
    for (int num : result4) {
        cout << num << " ";
    }
    cout << endl; // Expected output: -5 -1 -2 -3 -4

    return 0;
}

Output:

4 5 1 2 3
4 3 2
8 2 3 5
-4 -5 -1 -2 -3

Explanation of the said C++ code:

• The "reverse()" function takes a reference to a vector 'nums' and two integers 'start' and 'end' as parameters. It reverses the elements of the vector between the 'start' and 'end' indices. This function is used as a helper function to reverse portions of the array.
• The "rotateArray()" function takes a reference to a vector 'nums' and an integer 'k' as parameters. It first takes the modulo of 'k' with the size of the vector to ensure that 'k' is within the range of the vector length.
• The function then calls the "reverse()" function three times to perform the rotation:
• First, it reverses the entire array using "reverse(nums, 0, nums.size() - 1)".
• Then, it reverses the first 'k' elements of the array using "reverse(nums, 0, k - 1)".
• Finally, it reverses the remaining elements of the array using "reverse(nums, k, nums.size() - 1)".
• The "main()" function demonstrates the usage of the "rotateArray()" function with different test cases:
• It creates vectors 'arr1', 'arr2', 'arr3', and 'arr4' explicitly and rotates them using the "rotateArray()" function.
• It prints the rotated arrays to verify the correctness of the rotation.

C# - Rotate Array Solution:

Code:

using System;

class RotateArray
{
    public static int[] Rotate(int[] nums, int k)
    {
        // If k is greater than the length of nums, take its modulo
        k %= nums.Length;
        // Reverse the entire array
        Reverse(nums, 0, nums.Length - 1);
        // Reverse the first k elements
        Reverse(nums, 0, k - 1);
        // Reverse the remaining elements
        Reverse(nums, k, nums.Length - 1);
        return nums;
    }

    private static void Reverse(int[] nums, int start, int end)
    {
        // Helper function to reverse the array from start to end indices
        while (start < end)
        {
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start++;
            end--;
        }
    }

    static void Main(string[] args)
    {
        // Test cases
        int[] result1 = Rotate(new int[] { 1, 2, 3, 4, 5 }, 2);
        Console.WriteLine(string.Join(" ", result1)); // Expected output: 4 5 1 2 3

        int[] result2 = Rotate(new int[] { 3, 2, 4 }, 1);
        Console.WriteLine(string.Join(" ", result2)); // Expected output: 4 3 2

        int[] result3 = Rotate(new int[] { 3, 5, 8, 2 }, 10);
        Console.WriteLine(string.Join(" ", result3)); // Expected output: 8 2 3 5

        int[] result4 = Rotate(new int[] { -1, -2, -3, -4, -5 }, 7);
        Console.WriteLine(string.Join(" ", result4)); // Expected output: -5 -1 -2 -3 -4
    }
}

Output:

4 5 1 2 3
4 3 2
8 2 3 5
-4 -5 -1 -2 -3

Explanation of the said C# code:

• The "Rotate()" method takes two parameters: 'nums', an integer array to be rotated, and 'k', the number of steps to rotate the array to the right.
• To handle cases where 'k' is greater than the length of 'nums', the method calculates 'k' modulo the length of 'nums'. This ensures that 'k' is within the range of the array length.
• The method then calls the private static "Reverse()" method three times to perform the rotation:
• First, it reverses the entire array using "Reverse(nums, 0, nums.Length - 1)".
• Then, it reverses the first 'k' elements of the array using "Reverse(nums, 0, k - 1)".
• Finally, it reverses the remaining elements of the array using "Reverse(nums, k, nums.Length - 1)".
• The private static "Reverse()" method is a helper function that reverses the elements of the array between the 'start' and 'end' indices.
• The "Main()" method demonstrates the usage of the "Rotate()" method with different test cases:
• It calls the "Rotate()" method with arrays and respective rotation steps and prints the rotated arrays using "Console.WriteLine".

JavaScript - Rotate Array Solution:

Code:

function rotateArray(nums, k) {
    // If k is greater than the length of nums, take its modulo
    k %= nums.length;
    // Reverse the entire array
    reverse(nums, 0, nums.length - 1);
    // Reverse the first k elements
    reverse(nums, 0, k - 1);
    // Reverse the remaining elements
    reverse(nums, k, nums.length - 1);
    return nums;
}

function reverse(nums, start, end) {
    // Helper function to reverse the array from start to end indices
    while (start < end) {
        [nums[start], nums[end]] = [nums[end], nums[start]];
        start++;
        end--;
    }
}

// Test cases
console.log(rotateArray([1, 2, 3, 4, 5], 2));  // Expected output: [4, 5, 1, 2, 3]
console.log(rotateArray([3, 2, 4], 1));        // Expected output: [4, 3, 2]
console.log(rotateArray([3, 5, 8, 2], 10));     // Expected output: [8, 2, 3, 5]
console.log(rotateArray([-1, -2, -3, -4, -5], 7));  // Expected output: [-5, -1, -2, -3, -4]

Output:

[4, 5, 1, 2, 3]
[4, 3, 2]
[8, 2, 3, 5]
[-4, -5, -1, -2, -3]

Explanation of the said C# code:

• The "rotateArray()" function takes two parameters: 'nums', the array to be rotated, and 'k', the number of steps to rotate the array to the right.
• To handle cases where 'k' is greater than the length of 'nums', the function calculates 'k' modulo the length of 'nums'. This ensures that 'k' is within the range of the array length.
• The function then calls the "reverse()" function three times to perform the rotation:
• First, it reverses the entire array using "reverse(nums, 0, nums.length - 1)".
• Then, it reverses the first 'k' elements of the array using "reverse(nums, 0, k - 1)".
• Finally, it reverses the remaining elements of the array using "reverse(nums, k, nums.length - 1)".
• The "reverse()" function is a helper function that reverses the elements of the array between the 'start' and 'end' indices using array destructuring.
• The rotated array 'nums' is returned.

Time and Space Complexity:

Time Complexity:

• Reversal Operation: Reversing the entire array, reversing the first k elements, and reversing the remaining elements are all done in linear time, O(n), where n is the number of elements in the array.
• Overall: Since all operations are performed sequentially and each operation takes O(n) time, the overall time complexity is O(n).

Space Complexity:

• No Additional Space: The given solution doesn't use any extra space proportional to the input size. It operates directly on the input array in-place.
• Constant Space: Regardless of the size of the input array, the space used by the algorithm remains constant. It doesn't create any new arrays or data structures.
• Overall: Therefore, the space complexity of the solution is O(1).