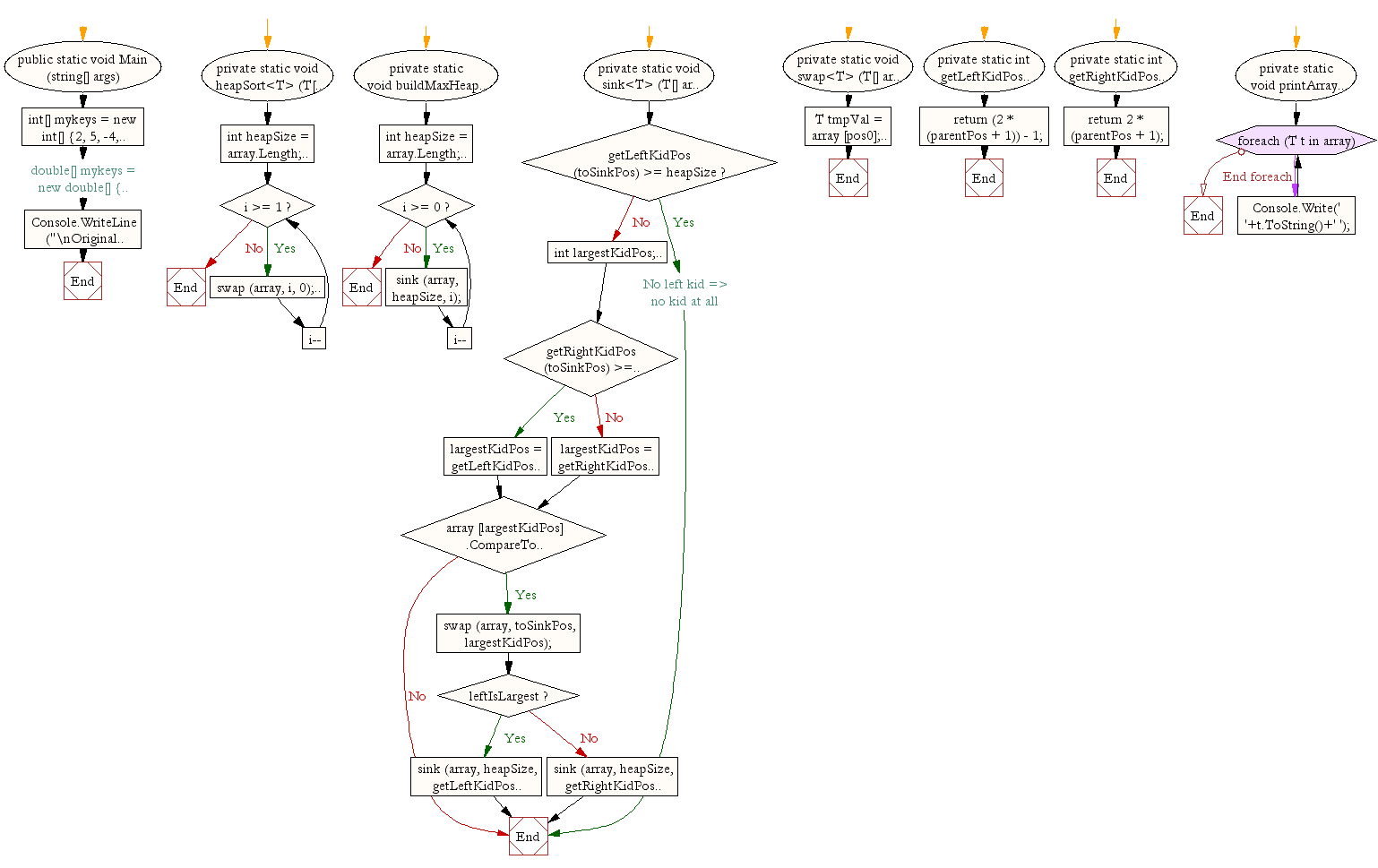
C#: Heap sort

C# Sharp Searching and Sorting Algorithm: Exercise-5 with Solution

Write a C# Sharp program to sort a list of elements using Heap sort.

In computer science, heapsort (invented by J. W. J. Williams in 1964) is a comparison-based sorting algorithm. Heapsort can be thought of as an improved selection sort: like that algorithm, it divides its input into a sorted and an unsorted region, and it interactively shrinks the unsorted region by extracting the largest element and moving that to the sorted region. The improvement consists of the use of a heap data structure rather than a linear-time search to find the maximum. Although somewhat slower in practice on most machines than a well-implemented quicksort, it has the advantage of a more favorable worst-case O(n log n) runtime. Heapsort is an in-place algorithm, but it is not a stable sort.

A run of the heapsort algorithm sorting an array of randomly permuted values. In the first stage of the algorithm the array elements are reordered to satisfy the heap property. Before the actual sorting takes place, the heap tree structure is shown briefly for illustration.

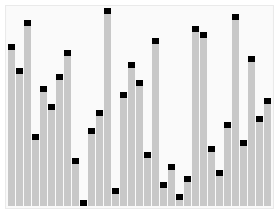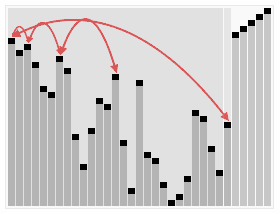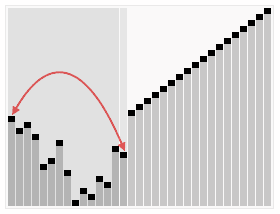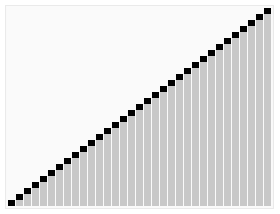
Animation credits : RolandH

Sample Solution:-

C# Sharp Code:

using System;

namespace Heap_sort
{
    public class MainClass
    {
        public static void Main(string[] args)
        {
            int[] mykeys = new int[] { 2, 5, -4, 11, 0, 18, 22, 67, 51, 6 };

            // Uncomment and use the following array types for testing:
            // double[] mykeys = new double[] {2.22, 0.5, 2.7, -1.0, 11.2};
            // string[] mykeys = new string[] {"Red", "White", "Black", "Green", "Orange"};

            Console.WriteLine("\nOriginal Array Elements :");
            printArray(mykeys); // Display the original array elements

            heapSort(mykeys); // Sort the array using Heap Sort

            Console.WriteLine("\n\nSorted Array Elements :");
            printArray(mykeys); // Display the sorted array elements
            Console.WriteLine("\n");
        }

        // Method to perform Heap Sort on an array of type T, which implements IComparable
        private static void heapSort<T>(T[] array) where T : IComparable<T>
        {
            int heapSize = array.Length;

            buildMaxHeap(array); // Build the max heap

            // Sorting by extracting elements from the heap
            for (int i = heapSize - 1; i >= 1; i--)
            {
                swap(array, i, 0); // Swap the first and last elements
                heapSize--;
                sink(array, heapSize, 0); // Restore the heap property
            }
        }

        // Method to build the max heap
        private static void buildMaxHeap<T>(T[] array) where T : IComparable<T>
        {
            int heapSize = array.Length;

            // Iterate over half the array elements and sink each one
            for (int i = (heapSize / 2) - 1; i >= 0; i--)
            {
                sink(array, heapSize, i); // Sink the element to maintain the heap property
            }
        }

        // Method to maintain the heap property
        private static void sink<T>(T[] array, int heapSize, int toSinkPos) where T : IComparable<T>
        {
            if (getLeftKidPos(toSinkPos) >= heapSize)
            {
                // No left kid => no kid at all
                return;
            }

            int largestKidPos;
            bool leftIsLargest;

            // Determine the largest kid
            if (getRightKidPos(toSinkPos) >= heapSize || array[getRightKidPos(toSinkPos)].CompareTo(array[getLeftKidPos(toSinkPos)]) < 0)
            {
                largestKidPos = getLeftKidPos(toSinkPos);
                leftIsLargest = true;
            }
            else
            {
                largestKidPos = getRightKidPos(toSinkPos);
                leftIsLargest = false;
            }

            // Swap the elements if necessary and sink recursively
            if (array[largestKidPos].CompareTo(array[toSinkPos]) > 0)
            {
                swap(array, toSinkPos, largestKidPos);
                if (leftIsLargest)
                {
                    sink(array, heapSize, getLeftKidPos(toSinkPos));
                }
                else
                {
                    sink(array, heapSize, getRightKidPos(toSinkPos));
                }
            }
        }

        // Method to swap two elements in the array
        private static void swap<T>(T[] array, int pos0, int pos1)
        {
            T tmpVal = array[pos0];
            array[pos0] = array[pos1];
            array[pos1] = tmpVal;
        }

        // Method to get the index of the left child of a parent node
        private static int getLeftKidPos(int parentPos)
        {
            return (2 * (parentPos + 1)) - 1;
        }

        // Method to get the index of the right child of a parent node
        private static int getRightKidPos(int parentPos)
        {
            return 2 * (parentPos + 1);
        }

        // Method to print the array elements
        private static void printArray<T>(T[] array)
        {
            foreach (T t in array)
            {
                Console.Write(' ' + t.ToString() + ' ');
            }
        }
    }
}

Sample Output:

Original Array Elements :                                                                                     
 2  5  -4  11  0  18  22  67  51  6                                                                           
                                                                                                              
Sorted Array Elements :                                                                                       
 -4  0  2  5  6  11  18  22  51  67  

Flowchart:

C# Sharp Practice online:

Contribute your code and comments through Disqus.

Previous: Write a C# Sharp program to sort a list of elements using Counting sort
Next: Write a C# Sharp program to sort a list of elements using Insertion sort.