C#: Generate all possible permutations of an array
Write a program in C# Sharp to generate all possible permutations of an array using recursion.
Visual Presentation:
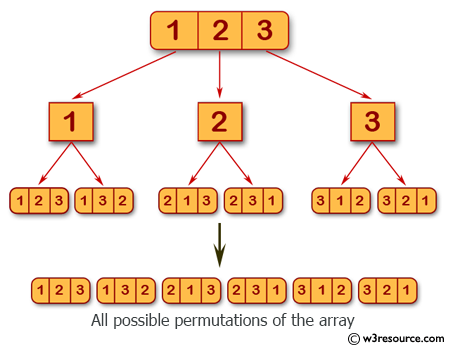
Sample Solution:
C# Sharp Code:
using System;
// Class formPermut contains methods to perform permutation operations
class formPermut
{
// Method to swap two numbers using pass-by-reference
public void swapTwoNumber(ref int a, ref int b)
{
int temp = a;
a = b;
b = temp;
}
// Method to generate permutations of elements in the array
public void prnPermut(int[] list, int k, int m)
{
int i;
// If k equals m, it signifies a complete permutation
if (k == m)
{
for (i = 0; i <= m; i++)
Console.Write("{0}", list[i]); // Print the permutation
Console.Write(" "); // Space after each permutation
}
else
{
// Loop to generate permutations
for (i = k; i <= m; i++)
{
swapTwoNumber(ref list[k], ref list[i]); // Swap elements at positions k and i
prnPermut(list, k + 1, m); // Recursively generate permutations for the remaining elements
swapTwoNumber(ref list[k], ref list[i]); // Restore the original order for backtracking
}
}
}
}
// Main class RecExercise11 to execute permutation generation
class RecExercise11
{
public static void Main()
{
int n, i;
formPermut test = new formPermut();
int[] arr1 = new int[5];
Console.WriteLine("\n\n Recursion : Generate all possible permutations of an array :");
Console.WriteLine("------------------------------------------------------------------");
// Accept user input for the number of elements in the array
Console.Write(" Input the number of elements to store in the array [maximum 5 digits]: ");
n = Convert.ToInt32(Console.ReadLine());
Console.Write(" Input {0} number of elements in the array:\n", n);
// Accept user input for array elements
for (i = 0; i < n; i++)
{
Console.Write(" element - {0} : ", i);
arr1[i] = Convert.ToInt32(Console.ReadLine());
}
// Display generated permutations of the array elements
Console.Write("\n The Permutations with a combination of {0} digits are: \n", n);
test.prnPermut(arr1, 0, n - 1);
Console.Write("\n\n");
}
}
Sample Output:
Recursion : Generate all possible permutations of an array :
------------------------------------------------------------------
Input the number of elements to store in the array [maximum 5 digits ] :3
Input 3 number of elements in the array :
element - 0 : 1
element - 1 : 2
element - 2 : 3
The Permutations with a combination of 3 digits are :
123 132 213 231 321 312
Flowchart :
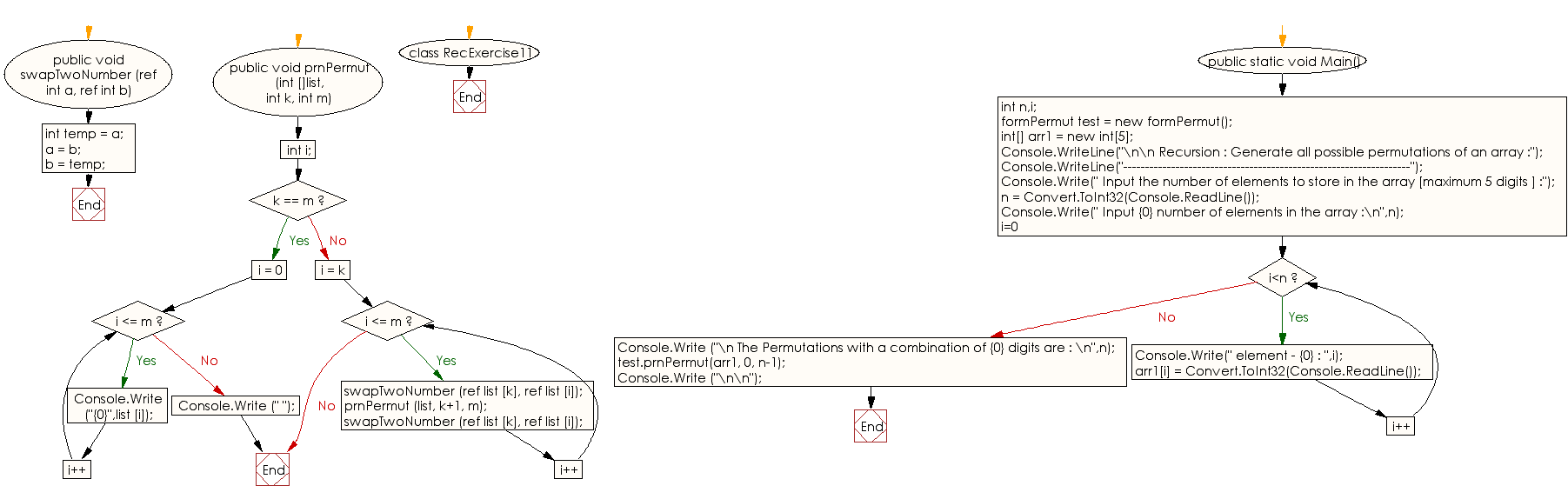
Go to:
PREV : Write a program in C# Sharp to find the Fibonacci numbers for a n numbers of series using recursion.
NEXT : Write a program in C# Sharp to find the LCM and GCD of two numbers using recursion.
C# Sharp Code Editor:
Improve this sample solution and post your code through Disqus
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
