C#: Calculate the value of e (Euler's number)

Last update on June 24 2025 12:58:06 (UTC/GMT +8 hours)

Calculate Euler's Number (e)

From Wikipedia,
The number e, also known as Euler's number, is a mathematical constant approximately equal to 2.71828 which can be characterized in many ways. It is the base of the natural logarithms. It is the limit of (1 + 1/n)n as n approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite series

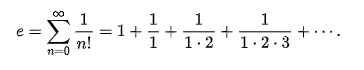
C# Sharp Exercises: mathematical_constant.

Write a C# Sharp program to calculate the value of e.
Note: e is also known as Euler's number and Napier's constant.

Sample Solution:

C# Sharp Code:

using System;

namespace exercises
{
    class Program
    {
        // Constant to define a very small value for comparison
        public const double EPSILON = 1.0e-15;

        static void Main(string[] args)
        {
            // Initialize variables
            ulong fact = 1;          // Initialize factorial value to 1
            double e = 2.0;         // Initialize the value of 'e' to 2.0
            double e0;              // Initialize a temporary variable to hold previous 'e' value
            uint n = 2;             // Initialize a counter 'n' starting from 2

            // Loop to calculate 'e' using a series approximation until the difference between successive 'e' values is less than EPSILON
            do
            {
                e0 = e;             // Store the current value of 'e' in 'e0'
                fact *= n++;        // Calculate the factorial incrementally and update 'n'
                e += 1.0 / fact;    // Update 'e' using the factorial value
            } while (Math.Abs(e - e0) >= EPSILON); // Continue the loop until the difference between current 'e' and previous 'e' is greater than or equal to EPSILON

            // Output the calculated value of 'e' with high precision
            Console.WriteLine("e = {0:F15}", e);
        }
    }
}

Sample Output:

e = 2.718281828459050

Flowchart:

For more Practice: Solve these Related Problems:

Write a C# program to calculate the value of e using factorials up to the 20th term.
Write a C# program to estimate Euler’s number with an error less than 0.0001 using a loop.
Write a C# program to approximate 'e' using infinite series until the difference between terms is negligible.
Write a C# program to calculate e raised to the power of x using Taylor Series expansion.

Go to:

PREV : Equality of Value and Type.
Next C# Sharp Exercise: Create Identity Matrix.

C# Sharp Code Editor: