C++ Recursion: Checking if a binary tree is a binary search tree

C++ Recursion: Exercise-15 with Solution

Write a C++ program to implement a recursive function to check if a given binary tree is a binary search tree.

In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is directly proportional to the height of the tree.

Visual Presentation:

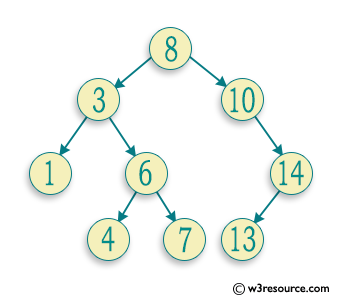
Sample Solution:

C Code:

#include <iostream>

// Structure for a binary tree node
struct Node {
  int data;
  Node * left;
  Node * right;

  // Constructor to initialize a node with a value
  Node(int value): data(value), left(nullptr), right(nullptr) {}
};

// Helper function to create a new node
Node * createNode(int value) {
  return new Node(value);
}

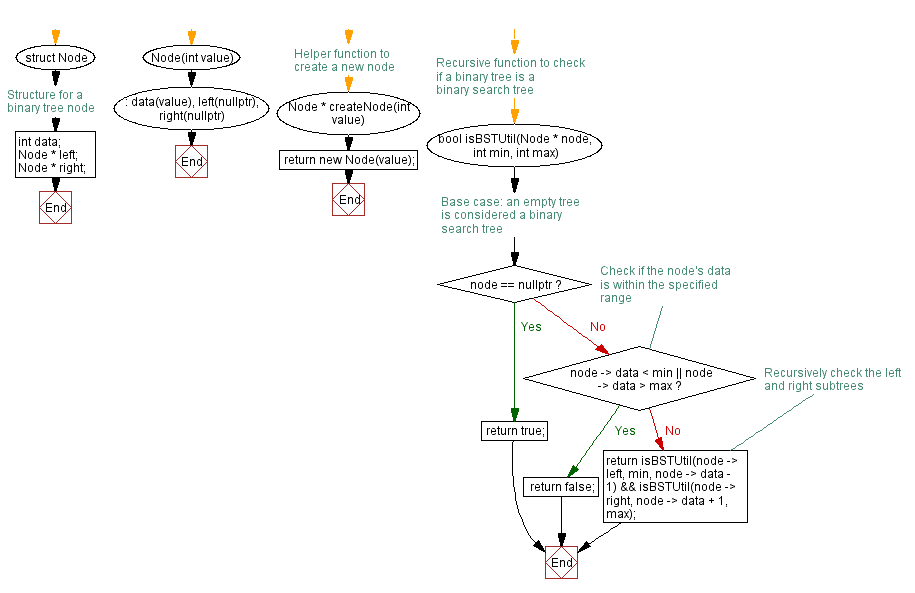
// Recursive function to check if a binary tree is a binary search tree
bool isBSTUtil(Node * node, int min, int max) {
  // Base case: an empty tree is considered a binary search tree
  if (node == nullptr)
    return true;

  // Check if the node's data is within the specified range
  if (node->data < min || node->data > max)
    return false;

  // Recursively check the left and right subtrees
  return isBSTUtil(node->left, min, node->data - 1) &&
         isBSTUtil(node->right, node->data + 1, max);
}

// Function to check if a binary tree is a binary search tree
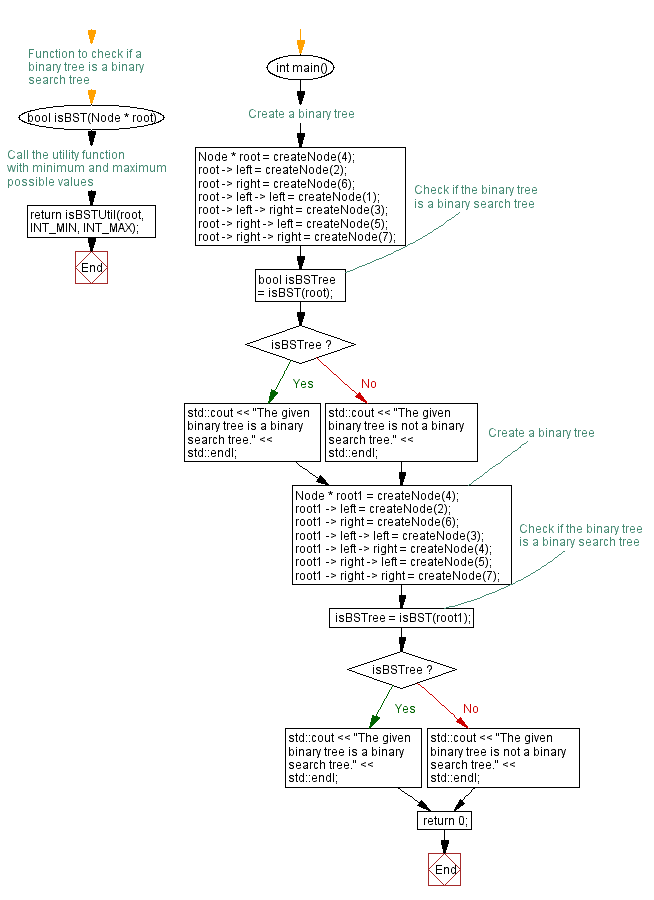
bool isBST(Node * root) {
  // Call the utility function with minimum and maximum possible values
  return isBSTUtil(root, INT_MIN, INT_MAX);
}

int main() {
  // Create a binary tree
  Node * root = createNode(4);
  root->left = createNode(2);
  root->right = createNode(6);
  root->left->left = createNode(1);
  root->left->right = createNode(3);
  root->right->left = createNode(5);
  root->right->right = createNode(7);

  // Check if the binary tree is a binary search tree
  bool isBSTree = isBST(root);
  if (isBSTree)
    std::cout << "The given binary tree is a binary search tree." << std::endl;
  else
    std::cout << "The given binary tree is not a binary search tree." << std::endl;

  // Create a binary tree
  Node * root1 = createNode(4);
  root1->left = createNode(2);
  root1->right = createNode(6);
  root1->left->left = createNode(3);
  root1->left->right = createNode(4);
  root1->right->left = createNode(5);
  root1->right->right = createNode(7);

  // Check if the binary tree is a binary search tree
  isBSTree = isBST(root1);

  if (isBSTree)
    std::cout << "The given binary tree is a binary search tree." << std::endl;
  else
    std::cout << "The given binary tree is not a binary search tree." << std::endl;

  return 0;
}

Sample Output:

The given binary tree is a binary search tree.
The given binary tree is not a binary search tree.

Explanation:

In the above exercise,

• The Node struct represents a node in the binary tree. The "createNode()" function is used to create a new node with the given value.
• The "isBSTUtil()" function is a recursive utility function that checks if a binary tree (with the given node as the root) is a binary search tree.
• The base case is when the node is nullptr, which is considered a binary search tree.
• The function checks if the node's data is within the specified range (between min and max). If it's not, it returns false.
• Otherwise, it recursively calls itself for the left subtree with the updated min and max values and for the right subtree with the updated min and max values. The function returns true only if both recursive calls return true.
• The "isBST()" function calls the "isBSTUtil()" function with initial minimum and maximum values (-infinity and +infinity).

The main function creates two binary tree, calls the "isBST()" function to check if the binary tree is a binary search tree, and then displays the result.

Flowchart:

CPP Code Editor:

Contribute your code and comments through Disqus.

Previous C++ Exercise: Calculating the sum of even and odd numbers in a range.
Next C++ Exercise: Sum of prime numbers in a range.