C++ Exercises: Check whether a given number is a perfect cube or not

Last update on April 12 2025 12:59:53 (UTC/GMT +8 hours)

32. Perfect Cube Check

Write a C++ program to check whether a given number is a perfect cube or not.

Sample Solution:

C++ Code :

#include<iostream> // Include input-output stream library
#include<math.h>   // Include math library for mathematical functions
using namespace std; // Use the standard namespace

int main() // Start of the main function
{ 
    int num, curoot, ans; // Declare variables to store the number, cube root, and answer

    cout << "\n\n Check whether a number is a perfect cube or not: \n"; // Display purpose
    cout << " -----------------------------------------------------\n"; // Display purpose
    cout << " Input a number: "; // Ask user for input
    cin >> num; // Read the input number from the user

    curoot = round(pow(num, 1.0/3.0)); // Calculate the cube root of the input number

    if(curoot * curoot * curoot == num) // Check if the number is a perfect cube
    {
        cout << " The number is a perfect Cube of " << curoot << endl; // Display if the number is a perfect cube
    }
    else
    {
        cout << " The number is not a perfect Cube." << endl; // Display if the number is not a perfect cube
    }
} // End of the main function

Sample Output:

Check whether a number is a perfect cube or not:                      
 -----------------------------------------------------                 
 Input a number: 8                                                     
 The number is a perfect Cube of 2

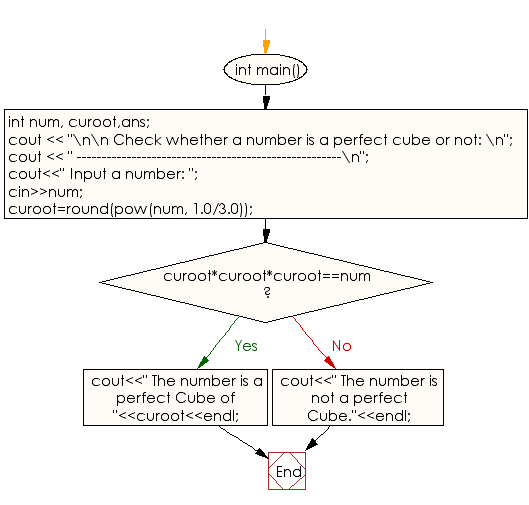
Flowchart:

For more Practice: Solve these Related Problems:

Write a C++ program to check if a number is a perfect cube by calculating its cube root and verifying integer status.
Write a C++ program to determine perfect cubes using a loop that tests cube values against the input.
Write a C++ program to verify if a number is a perfect cube using floating-point comparison with tolerance.
Write a C++ program to check perfect cube status by converting the cube root result to an integer and back.

C++ Code Editor:

Contribute your code and comments through Disqus.

Previous: Write a program in C++ to find circular prime numbers upto a specific limit.
Next: Write a program in C++ to display first 10 Fermat numbers.