C++ Exercises: Calculate the sum of the series (1*1) + (2*2) + (3*3) + (4*4) + (5*5) + ... + (n*n)

Last update on April 07 2025 12:59:45 (UTC/GMT +8 hours)

12. Sum of the Series (1*1) + (2*2) + ... + (n*n)

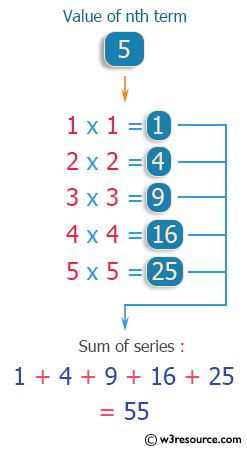
Write a program in C++ to calculate the sum of the series (1*1) + (2*2) + (3*3) + (4*4) + (5*5) + ... + (n*n).

Visual Presentation:

Sample Solution :-

C++ Code :

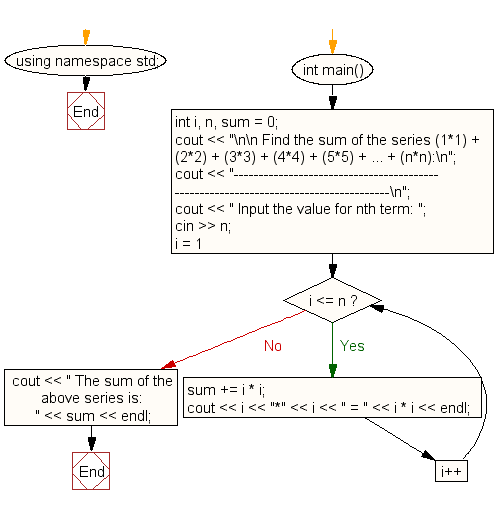
#include <iostream> // Including the input/output stream header file

using namespace std; // Using the standard namespace to avoid writing std::

int main() // Start of the main function
{
    int i, n, sum = 0; // Declaration of integer variables 'i', 'n', and 'sum'

    // Display a message to find the sum of the series (1*1) + (2*2) + (3*3) + (4*4) + (5*5) + ... + (n*n)
    cout << "\n\n Find the sum of the series (1*1) + (2*2) + (3*3) + (4*4) + (5*5) + ... + (n*n):\n";
    cout << "------------------------------------------------------------------------------------\n";

    // Prompt the user to input the value for the nth term of the series
    cout << " Input the value for nth term: ";
    cin >> n; // Read the value entered by the user

    for (i = 1; i <= n; i++) // Loop to calculate each term of the series
	{
        sum += i * i; // Calculate the square of 'i' and add it to the sum
        cout << i << "*" << i << " = " << i * i << endl; // Display the current term as i*i
    }

    // Display the total sum of the series
    cout << " The sum of the above series is: " << sum << endl;

    return 0; // Indicating successful completion of the program
}

Sample Output:

 Find the sum of the series (1*1) + (2*2) + (3*3) + (4*4) + (5*5) + ...
 + (n*n):                                                              
-----------------------------------------------------------------------
-------------                                                          
 Input the value for nth term: 5                                       
1*1 = 1                                                                
2*2 = 4                                                                
3*3 = 9                                                                
4*4 = 16                                                               
5*5 = 25                                                               
 The sum of the above series is: 55  

Flowchart:

For more Practice: Solve these Related Problems:

• Write a C++ program to calculate the sum of squares of the first n natural numbers using a loop.
• Write a C++ program that computes the series 1² + 2² + ... + n² and prints both each square and the total sum.
• Write a C++ program to determine the sum of the squares of numbers from 1 to n using the formula and compare it with a loop-based calculation.
• Write a C++ program that reads n and then outputs the sum of squares from 1 to n along with the individual square values.

C++ Code Editor:

Click to Open Editor

Contribute your code and comments through Disqus.

Previous: Write a program in C++ to find the sum of the series 1 + 1/2^2 + 1/3^3 + …..+ 1/n^n.
Next: Write a program in C++ to calculate the series (1) + (1+2) + (1+2+3) + (1+2+3+4) + ... + (1+2+3+4+...+n).