C++ Exercises: Check whether the sequence of the numbers in a given array is a “Arithmetic” or “Geometric” sequence

C++ Basic: Exercise-84 with Solution

Check Arithmetic or Geometric Sequence

Write a C++ program to check whether the sequence of the numbers in a given array is an "Arithmetic" or "Geometric" sequence. Return -1 if the sequence is not "Arithmetic" or "Geometric".

From Wikipedia
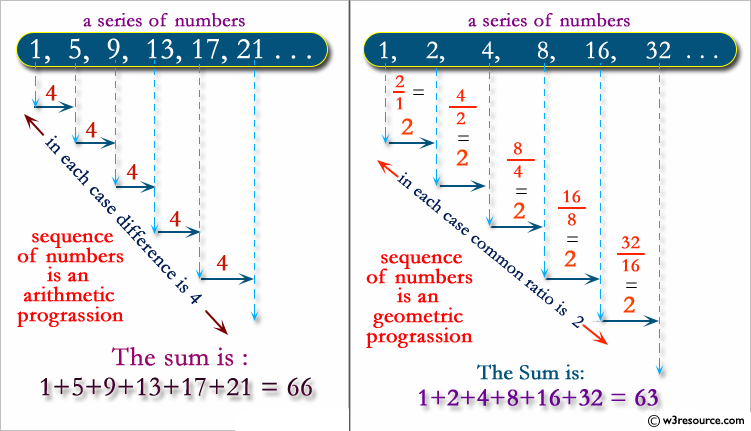
In mathematics, an arithmetic progression (AP) or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant. Difference here means the second minus the first. For instance, the sequence 5, 7, 9, 11, 13, 15, . . . is an arithmetic progression with common difference of 2.
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio 1/2.

Visual Presentation:

Sample Solution:

C++ Code :

#include <iostream>
#include <string>

using namespace std;

// Function to identify arithmetic or geometric sequences
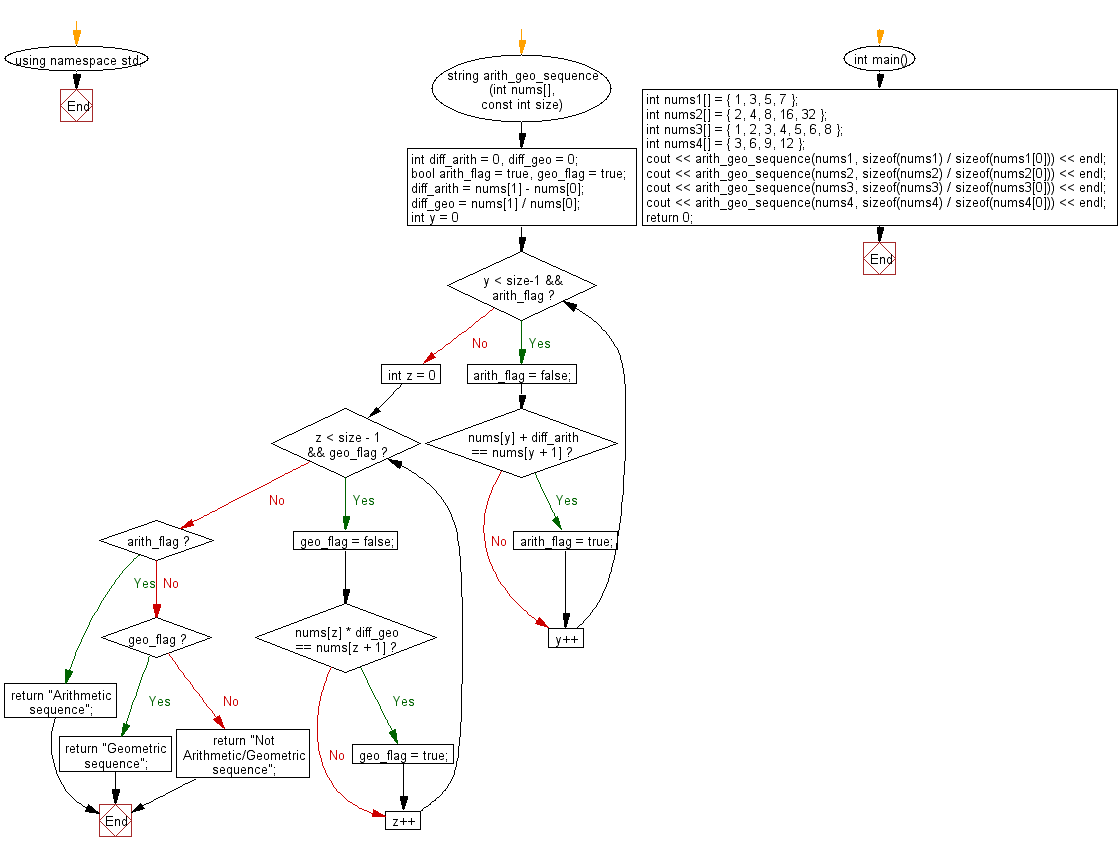
string arith_geo_sequence(int nums[], const int size) {

    // Variables to hold differences for arithmetic and geometric sequences
    int diff_arith = 0, diff_geo = 0;
    // Flags to identify if the sequence is arithmetic or geometric
    bool arith_flag = true, geo_flag = true;

    // Calculate differences between consecutive elements
    diff_arith = nums[1] - nums[0];
    diff_geo = nums[1] / nums[0];

    // Check for arithmetic sequence
    for (int y = 0; y < size - 1 && arith_flag; y++) {
        arith_flag = false;

        if (nums[y] + diff_arith == nums[y + 1]) {
            arith_flag = true;
        }
    }

    // Check for geometric sequence
    for (int z = 0; z < size - 1 && geo_flag; z++) {
        geo_flag = false;

        if (nums[z] * diff_geo == nums[z + 1]) {
            geo_flag = true;
        }
    }

    // Return appropriate result based on the identified sequence
    if (arith_flag) {
        return "Arithmetic sequence";
    } else if (geo_flag) {
        return "Geometric sequence";
    } else {
        return "Not Arithmetic/Geometric sequence";
    }
}

int main() {
    // Different arrays to test for arithmetic or geometric sequence
    int nums1[] = { 1, 3, 5, 7 };
    int nums2[] = { 2, 4, 8, 16, 32 };
    int nums3[] = { 1, 2, 3, 4, 5, 6, 8 };
    int nums4[] = { 3, 6, 9, 12 };

    // Function calls to identify sequence types for each array and print the result
    cout << arith_geo_sequence(nums1, sizeof(nums1) / sizeof(nums1[0])) << endl;
    cout << arith_geo_sequence(nums2, sizeof(nums2) / sizeof(nums2[0])) << endl;
    cout << arith_geo_sequence(nums3, sizeof(nums3) / sizeof(nums3[0])) << endl;
    cout << arith_geo_sequence(nums4, sizeof(nums4) / sizeof(nums4[0])) << endl;

    return 0;
}

Sample Output:

Arithmetic sequence
Geometric sequence
Not Arithmetic/Geometric sequence
Arithmetic sequence

Flowchart:

C++ Code Editor:

Previous: Write a C++ program which reads a list of pairs of a word and a page number, and prints the word and a list of the corresponding page numbers.
Next: Write a C++ program find the total number of minutes between two given times.