Implementing AVL Tree in C: Insertion and Deletion Operations
10. AVL Tree Implementation Extensions
Write a C program that implements an AVL tree in C. Include functions for insertion and deletion while maintaining the AVL tree's balance property.
In computer science, an AVL tree (named after inventors Adelson-Velsky and Landis) is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.
Sample Solution:
C Code:
// Including necessary header files
#include <stdio.h>
#include <stdlib.h>
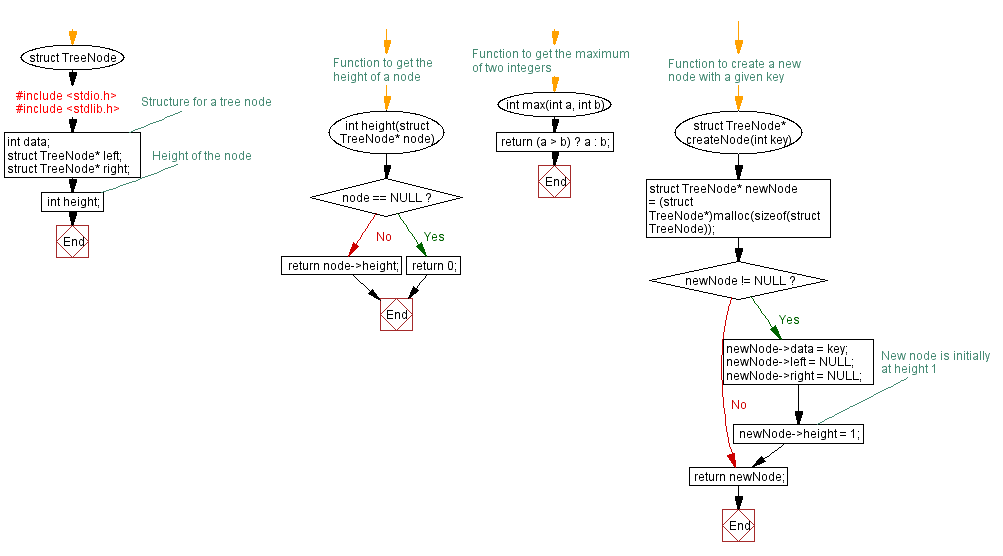
// Structure for a tree node
struct TreeNode {
int data;
struct TreeNode* left;
struct TreeNode* right;
int height; // Height of the node
};
// Function to get the height of a node
int height(struct TreeNode* node) {
if (node == NULL)
return 0;
return node->height;
}
// Function to get the maximum of two integers
int max(int a, int b) {
return (a > b) ? a : b;
}
// Function to create a new node with a given key
struct TreeNode* createNode(int key) {
struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
if (newNode != NULL) {
newNode->data = key;
newNode->left = NULL;
newNode->right = NULL;
newNode->height = 1; // New node is initially at height 1
}
return newNode;
}
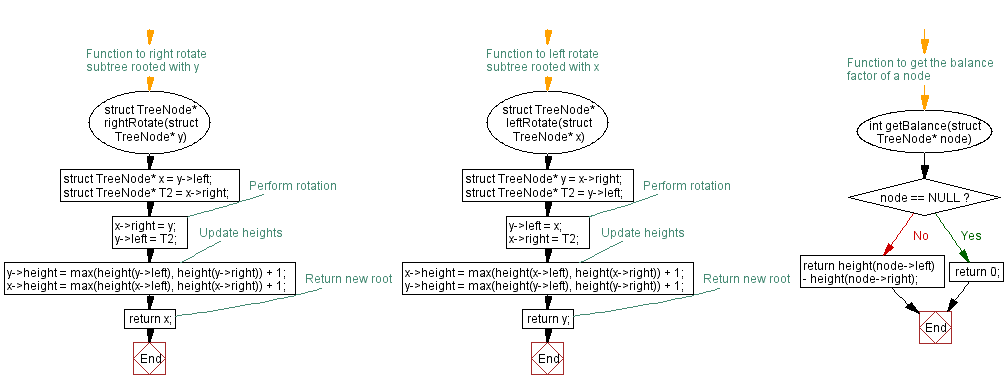
// Function to right rotate subtree rooted with y
struct TreeNode* rightRotate(struct TreeNode* y) {
struct TreeNode* x = y->left;
struct TreeNode* T2 = x->right;
// Perform rotation
x->right = y;
y->left = T2;
// Update heights
y->height = max(height(y->left), height(y->right)) + 1;
x->height = max(height(x->left), height(x->right)) + 1;
// Return new root
return x;
}
// Function to left rotate subtree rooted with x
struct TreeNode* leftRotate(struct TreeNode* x) {
struct TreeNode* y = x->right;
struct TreeNode* T2 = y->left;
// Perform rotation
y->left = x;
x->right = T2;
// Update heights
x->height = max(height(x->left), height(x->right)) + 1;
y->height = max(height(y->left), height(y->right)) + 1;
// Return new root
return y;
}
// Function to get the balance factor of a node
int getBalance(struct TreeNode* node) {
if (node == NULL)
return 0;
return height(node->left) - height(node->right);
}
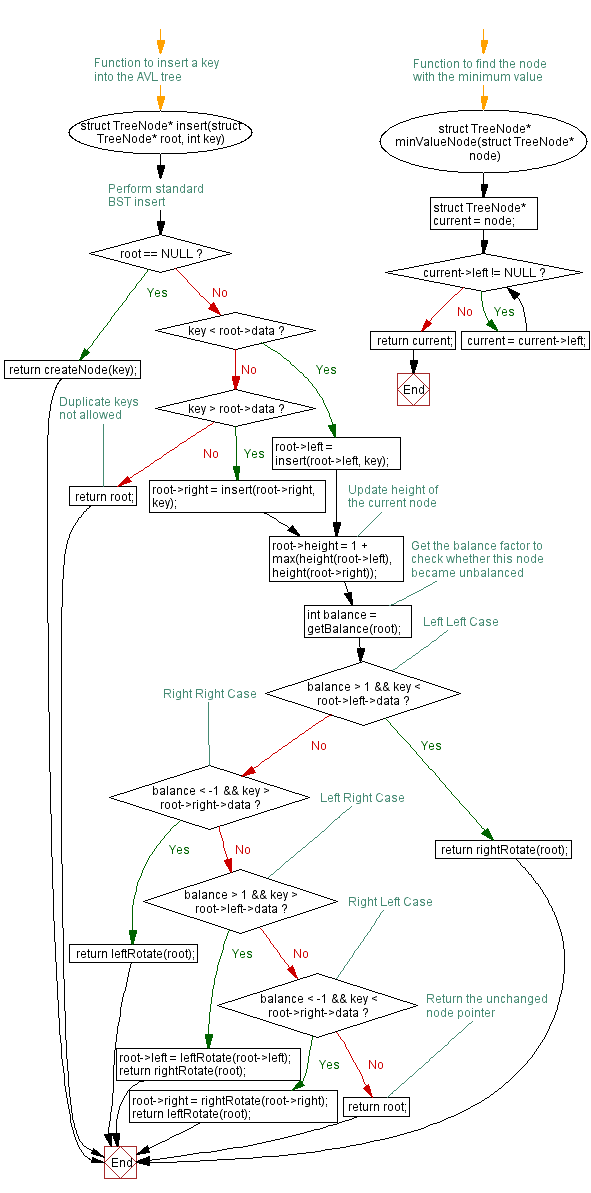
// Function to insert a key into the AVL tree
struct TreeNode* insert(struct TreeNode* root, int key) {
// Perform standard BST insert
if (root == NULL)
return createNode(key);
if (key < root->data)
root->left = insert(root->left, key);
else if (key > root->data)
root->right = insert(root->right, key);
else // Duplicate keys not allowed
return root;
// Update height of the current node
root->height = 1 + max(height(root->left), height(root->right));
// Get the balance factor to check whether this node became unbalanced
int balance = getBalance(root);
// Left Left Case
if (balance > 1 && key < root->left->data)
return rightRotate(root);
// Right Right Case
if (balance < -1 && key > root->right->data)
return leftRotate(root);
// Left Right Case
if (balance > 1 && key > root->left->data) {
root->left = leftRotate(root->left);
return rightRotate(root);
}
// Right Left Case
if (balance < -1 && key < root->right->data) {
root->right = rightRotate(root->right);
return leftRotate(root);
}
// Return the unchanged node pointer
return root;
}
// Function to find the node with the minimum value
struct TreeNode* minValueNode(struct TreeNode* node) {
struct TreeNode* current = node;
while (current->left != NULL)
current = current->left;
return current;
}
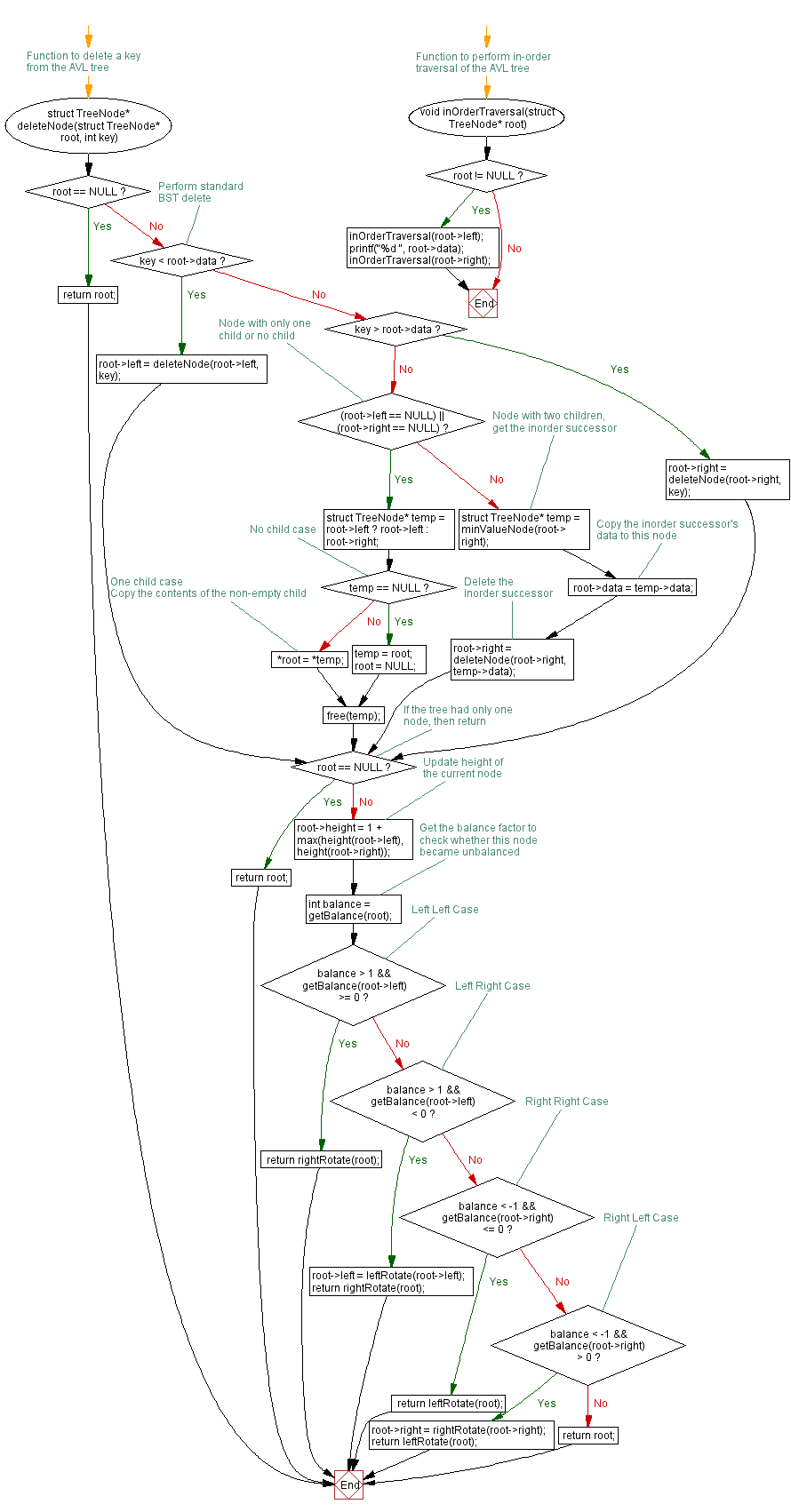
// Function to delete a key from the AVL tree
struct TreeNode* deleteNode(struct TreeNode* root, int key) {
if (root == NULL)
return root;
// Perform standard BST delete
if (key < root->data)
root->left = deleteNode(root->left, key);
else if (key > root->data)
root->right = deleteNode(root->right, key);
else {
// Node with only one child or no child
if ((root->left == NULL) || (root->right == NULL)) {
struct TreeNode* temp = root->left ? root->left : root->right;
// No child case
if (temp == NULL) {
temp = root;
root = NULL;
} else // One child case
*root = *temp; // Copy the contents of the non-empty child
free(temp);
} else {
// Node with two children, get the inorder successor
struct TreeNode* temp = minValueNode(root->right);
// Copy the inorder successor's data to this node
root->data = temp->data;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->data);
}
}
// If the tree had only one node, then return
if (root == NULL)
return root;
// Update height of the current node
root->height = 1 + max(height(root->left), height(root->right));
// Get the balance factor to check whether this node became unbalanced
int balance = getBalance(root);
// Left Left Case
if (balance > 1 && getBalance(root->left) >= 0)
return rightRotate(root);
// Left Right Case
if (balance > 1 && getBalance(root->left) < 0) {
root->left = leftRotate(root->left);
return rightRotate(root);
}
// Right Right Case
if (balance < -1 && getBalance(root->right) <= 0)
return leftRotate(root);
// Right Left Case
if (balance < -1 && getBalance(root->right) > 0) {
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// Function to perform in-order traversal of the AVL tree
void inOrderTraversal(struct TreeNode* root) {
if (root != NULL) {
inOrderTraversal(root->left);
printf("%d ", root->data);
inOrderTraversal(root->right);
}
}
// Function to free the memory allocated for the AVL tree
void freeAVLTree(struct TreeNode* root) {
if (root != NULL) {
freeAVLTree(root->left);
freeAVLTree(root->right);
free(root);
}
}
int main() {
struct TreeNode* root = NULL;
int choice, key;
do {
printf("\nAVL Tree Operations:\n");
printf("1. Insert a node\n");
printf("2. Delete a node\n");
printf("3. In-order Traversal\n");
printf("4. Exit\n");
printf("Enter your choice: ");
scanf("%d", &choice);
switch (choice) {
case 1:
printf("Enter the key to insert: ");
scanf("%d", &key);
root = insert(root, key);
break;
case 2:
printf("Enter the key to delete: ");
scanf("%d", &key);
root = deleteNode(root, key);
break;
case 3:
printf("In-order Traversal: ");
inOrderTraversal(root);
printf("\n");
break;
case 4:
// Free allocated memory
freeAVLTree(root);
printf("Exiting...\n");
break;
default:
printf("Invalid choice! Please enter a valid option.\n");
}
} while (choice != 4);
return 0;
}
Output:
AVL Tree Operations: 1. Insert a node 2. Delete a node 3. In-order Traversal 4. Exit Enter your choice: 1 Enter the key to insert: 87 AVL Tree Operations: 1. Insert a node 2. Delete a node 3. In-order Traversal 4. Exit Enter your choice: 3 In-order Traversal: 87 AVL Tree Operations: 1. Insert a node 2. Delete a node 3. In-order Traversal 4. Exit Enter your choice: 1 Enter the key to insert: 45 AVL Tree Operations: 1. Insert a node 2. Delete a node 3. In-order Traversal 4. Exit Enter your choice: 1 Enter the key to insert: 34 AVL Tree Operations: 1. Insert a node 2. Delete a node 3. In-order Traversal 4. Exit Enter your choice: 3 In-order Traversal: 34 45 87 AVL Tree Operations: 1. Insert a node 2. Delete a node 3. In-order Traversal 4. Exit Enter your choice: 2 Enter the key to delete: 87 AVL Tree Operations: 1. Insert a node 2. Delete a node 3. In-order Traversal 4. Exit Enter your choice: 3 In-order Traversal: 34 45 AVL Tree Operations: 1. Insert a node 2. Delete a node 3. In-order Traversal 4. Exit Enter your choice: 4 Exiting...
Explanation:
In the exercise above,
Here's a brief explanation:
- Node Structure (struct TreeNode):
- Represents a node in the AVL tree.
- Contains data, left child, right child, and the height of the node.
- Utility Functions:
- height: Calculates the height of a node.
- max: Returns the maximum of two integers.
- createNode: Creates a new node with a given key.
- rightRotate and leftRotate: Perform right and left rotations, respectively, during balancing.
- Insertion (insert function):
- Inserts a new key into the AVL tree while maintaining the balance property.
- Utilizes rotations to ensure the tree remains balanced.
- Deletion (deleteNode function):
- Deletes a node with a given key while maintaining the balance property.
- Performs rotations to rebalance the tree as needed.
- In-order Traversal (inOrderTraversal function):
- Prints the elements of the AVL tree in sorted order (in-order traversal).
- Main Function:
- Interactively allows the user to perform AVL tree operations:
- Insert a node
- Delete a node
- In-order traversal
- Exit
- Freeing Memory (freeAVLTree function):
- Frees the memory allocated for the entire AVL tree.
Flowchart:
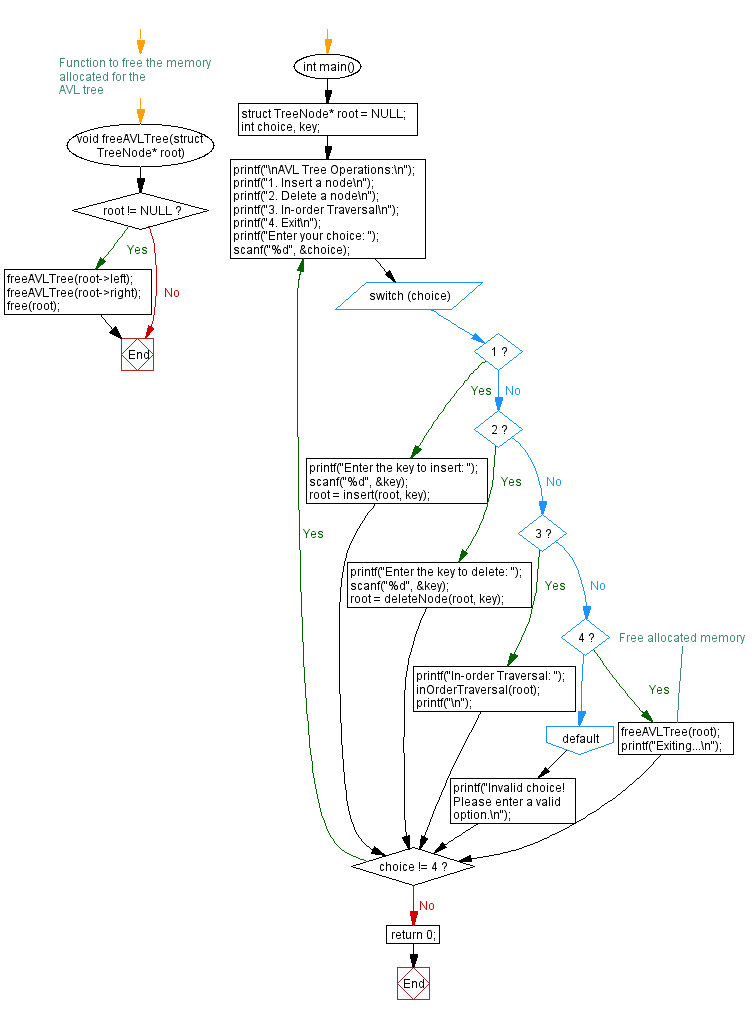
For more Practice: Solve these Related Problems:
- Write a C program to implement AVL tree insertion and display the number of rotations performed during each insertion.
- Write a C program to implement AVL tree deletion and then verify the balance factors of all nodes post-deletion.
- Write a C program to augment an AVL tree with a range query function that retrieves all keys within a specified interval.
- Write a C program to compare the performance of AVL tree operations with a standard BST under various input sequences.
Go to:
PREV : Root-to-Leaf Path Sum Challenges.
NEXT : C Programming Graph Structure and Algorithms Exercises Home.C Programming Code Editor:
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
