C Exercises: Sort numbers using Multi-key quicksort method
23. Multi-key Quicksort Variants
Write a C program that sorts numbers using the Multi-key quicksort method.
Multi-key quicksort, also known as three-way radix quicksort, is an algorithm for sorting strings. This hybrid of quicksort and radix sort was originally suggested by P. Shackleton, as reported in one of C.A.R. Hoare's seminal papers on quicksort, its modern incarnation was developed by Jon Bentley and Robert Sedgewick in the mid-1990s. The algorithm is designed to exploit the property that in many problems, strings tend to have shared prefixes.
Sample Solution:
Sample C Code:
//Sourec: https://bit.ly/3ejSWtP
# include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
// MULTIKEY QUICKSORT
#ifndef min
#define min(a, b) ((a) <= (b) ? (a) : (b))
#endif
#define swap(a, b) \
{ \
char *t = x[a]; \
x[a] = x[b]; \
x[b] = t; \
}
#define i2c(i) x[i][depth]
void vecswap(int i, int j, int n, char *x[])
{
while (n-- > 0)
{
swap(i, j);
i++;
j++;
}
}
void ssort1(char *x[], int n, int depth)
{
int a, b, c, d, r, v;
if (n <= 1)
return;
a = rand() % n;
swap(0, a);
v = i2c(0);
a = b = 1;
c = d = n - 1;
for (;;)
{
while (b <= c && (r = i2c(b) - v) <= 0)
{
if (r == 0)
{
swap(a, b);
a++;
}
b++;
}
while (b <= c && (r = i2c(c) - v) >= 0)
{
if (r == 0)
{
swap(c, d);
d--;
}
c--;
}
if (b > c)
break;
swap(b, c);
b++;
c--;
}
r = min(a, b - a);
vecswap(0, b - r, r, x);
r = min(d - c, n - d - 1);
vecswap(b, n - r, r, x);
r = b - a;
ssort1(x, r, depth);
if (i2c(r) != 0)
ssort1(x + r, a + n - d - 1, depth + 1);
r = d - c;
ssort1(x + n - r, r, depth);
}
void ssort1main(char *x[], int n) { ssort1(x, n, 0); }
// ssort2 -- Faster Version of Multikey Quicksort
void vecswap2(char **a, char **b, int n)
{
while (n-- > 0)
{
char *t = *a;
*a++ = *b;
*b++ = t;
}
}
#define swap2(a, b) \
{ \
t = *(a); \
*(a) = *(b); \
*(b) = t; \
}
#define ptr2char(i) (*(*(i) + depth))
char **med3func(char **a, char **b, char **c, int depth)
{
int va, vb, vc;
if ((va = ptr2char(a)) == (vb = ptr2char(b)))
return a;
if ((vc = ptr2char(c)) == va || vc == vb)
return c;
return va < vb ? (vb < vc ? b : (va < vc ? c : a))
: (vb > vc ? b : (va < vc ? a : c));
}
#define med3(a, b, c) med3func(a, b, c, depth)
void inssort(char **a, int n, int d)
{
char **pi, **pj, *s, *t;
for (pi = a + 1; --n > 0; pi++)
for (pj = pi; pj > a; pj--)
{
// Inline strcmp: break if *(pj-1) <= *pj
for (s = *(pj - 1) + d, t = *pj + d; *s == *t && *s != 0; s++, t++)
;
if (*s <= *t)
break;
swap2(pj, pj - 1);
}
}
void ssort2(char **a, int n, int depth)
{
int d, r, partval;
char **pa, **pb, **pc, **pd, **pl, **pm, **pn, *t;
if (n < 10)
{
inssort(a, n, depth);
return;
}
pl = a;
pm = a + (n / 2);
pn = a + (n - 1);
if (n > 30)
{ // On big arrays, pseudomedian of 9
d = (n / 8);
pl = med3(pl, pl + d, pl + 2 * d);
pm = med3(pm - d, pm, pm + d);
pn = med3(pn - 2 * d, pn - d, pn);
}
pm = med3(pl, pm, pn);
swap2(a, pm);
partval = ptr2char(a);
pa = pb = a + 1;
pc = pd = a + n - 1;
for (;;)
{
while (pb <= pc && (r = ptr2char(pb) - partval) <= 0)
{
if (r == 0)
{
swap2(pa, pb);
pa++;
}
pb++;
}
while (pb <= pc && (r = ptr2char(pc) - partval) >= 0)
{
if (r == 0)
{
swap2(pc, pd);
pd--;
}
pc--;
}
if (pb > pc)
break;
swap2(pb, pc);
pb++;
pc--;
}
pn = a + n;
r = min(pa - a, pb - pa);
vecswap2(a, pb - r, r);
r = min(pd - pc, pn - pd - 1);
vecswap2(pb, pn - r, r);
if ((r = pb - pa) > 1)
ssort2(a, r, depth);
if (ptr2char(a + r) != 0)
ssort2(a + r, pa - a + pn - pd - 1, depth + 1);
if ((r = pd - pc) > 1)
ssort2(a + n - r, r, depth);
}
void ssort2main(char **a, int n) { ssort2(a, n, 0); }
// TERNARY SEARCH TREE ALGS
typedef struct tnode *Tptr;
typedef struct tnode
{
char splitchar;
Tptr lokid, eqkid, hikid;
} Tnode;
Tptr root;
// Insert 1 -- Simple Insertion Algorithm
Tptr insert1(Tptr p, char *s)
{
if (p == 0)
{
p = (Tptr)malloc(sizeof(Tnode));
p->splitchar = *s;
p->lokid = p->eqkid = p->hikid = 0;
}
if (*s < p->splitchar)
p->lokid = insert1(p->lokid, s);
else if (*s == p->splitchar)
{
if (*s != 0)
p->eqkid = insert1(p->eqkid, ++s);
}
else
p->hikid = insert1(p->hikid, s);
return p;
}
void cleanup1(Tptr p)
{
if (p)
{
cleanup1(p->lokid);
cleanup1(p->eqkid);
cleanup1(p->hikid);
free(p);
}
}
// Insert 2 -- Faster version of Insert
#define BUFSIZE 1000
Tptr buffer;
int bufn, freen;
void *freearr[10000];
int storestring = 0;
void insert2(char *s)
{
int d;
char *instr = s;
Tptr pp, *p;
p = &root;
pp = *p;
while (pp == *p)
{
if ((d = *s - pp->splitchar) == 0)
{
if (*s++ == 0)
return;
p = &(pp->eqkid);
}
else if (d < 0)
p = &(pp->lokid);
else
p = &(pp->hikid);
}
for (;;)
{
// *p = (Tptr) malloc(sizeof(Tnode));
if (bufn-- == 0)
{
buffer = (Tptr)malloc(BUFSIZE * sizeof(Tnode));
freearr[freen++] = (void *)buffer;
bufn = BUFSIZE - 1;
}
*p = buffer++;
pp = *p;
pp->splitchar = *s;
pp->lokid = pp->eqkid = pp->hikid = 0;
if (*s++ == 0)
{
if (storestring)
pp->eqkid = (Tptr)instr;
return;
}
p = &(pp->eqkid);
}
}
void cleanup2()
{
int i;
for (i = 0; i < freen; i++) free(freearr[i]);
}
// Search Algorithms
int search1(char *s)
{
Tptr p;
p = root;
while (p)
{
if (*s < p->splitchar)
p = p->lokid;
else if (*s == p->splitchar)
{
if (*s++ == 0)
return 1;
p = p->eqkid;
}
else
p = p->hikid;
}
return 0;
}
int search2(char *s)
{
int d, sc;
Tptr p;
sc = *s;
p = root;
while (p)
{
if ((d = sc - p->splitchar) == 0)
{
if (sc == 0)
return 1;
sc = *++s;
p = p->eqkid;
}
else if (d < 0)
p = p->lokid;
else
p = p->hikid;
}
return 0;
}
// Advanced searching: Partial match, near words
int nodecnt;
char *srcharr[100000];
int srchtop;
void pmsearch(Tptr p, char *s)
{
if (!p)
return;
nodecnt++;
if (*s == '.' || *s < p->splitchar)
pmsearch(p->lokid, s);
if (*s == '.' || *s == p->splitchar)
if (p->splitchar && *s)
pmsearch(p->eqkid, s + 1);
if (*s == 0 && p->splitchar == 0)
srcharr[srchtop++] = (char *)p->eqkid;
if (*s == '.' || *s > p->splitchar)
pmsearch(p->hikid, s);
}
void nearsearch(Tptr p, char *s, int d)
{
if (!p || d < 0)
return;
nodecnt++;
if (d > 0 || *s < p->splitchar)
nearsearch(p->lokid, s, d);
if (p->splitchar == 0)
{
if ((int)strlen(s) <= d)
srcharr[srchtop++] = (char *)p->eqkid;
}
else
nearsearch(p->eqkid, *s ? s + 1 : s, (*s == p->splitchar) ? d : d - 1);
if (d > 0 || *s > p->splitchar)
nearsearch(p->hikid, s, d);
}
#define NUMBER_OF_STRING 3
int main(int argc, char *argv[])
{
char *arr[NUMBER_OF_STRING] = {"apple", "cat", "boy"};
ssort1main(arr, NUMBER_OF_STRING);
for (int i = 0; i < NUMBER_OF_STRING; i++)
{
printf("%s ", arr[i]);
}
}
Sample Output:
apple boy cat -------------------------------- Process exited after 0.3622 seconds with return value 0 Press any key to continue . . .
Flowchart:
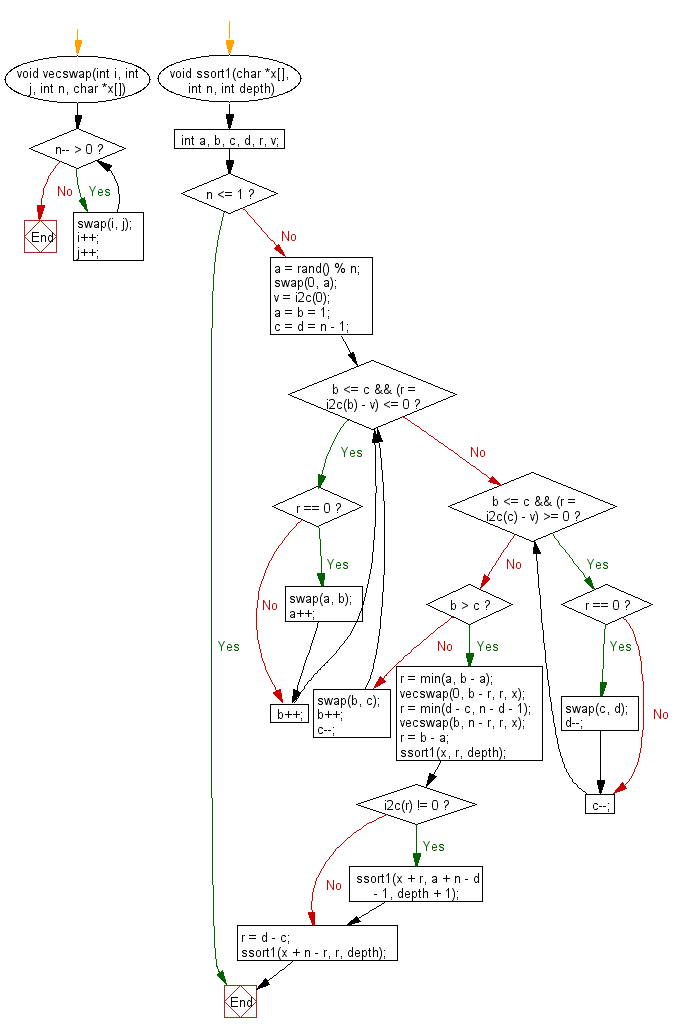
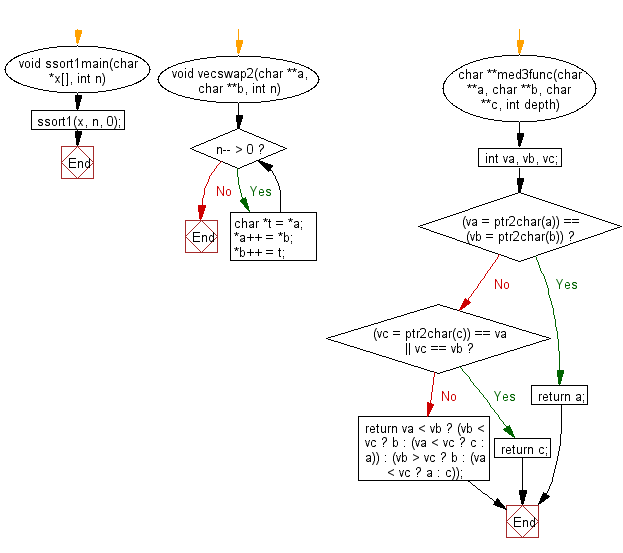
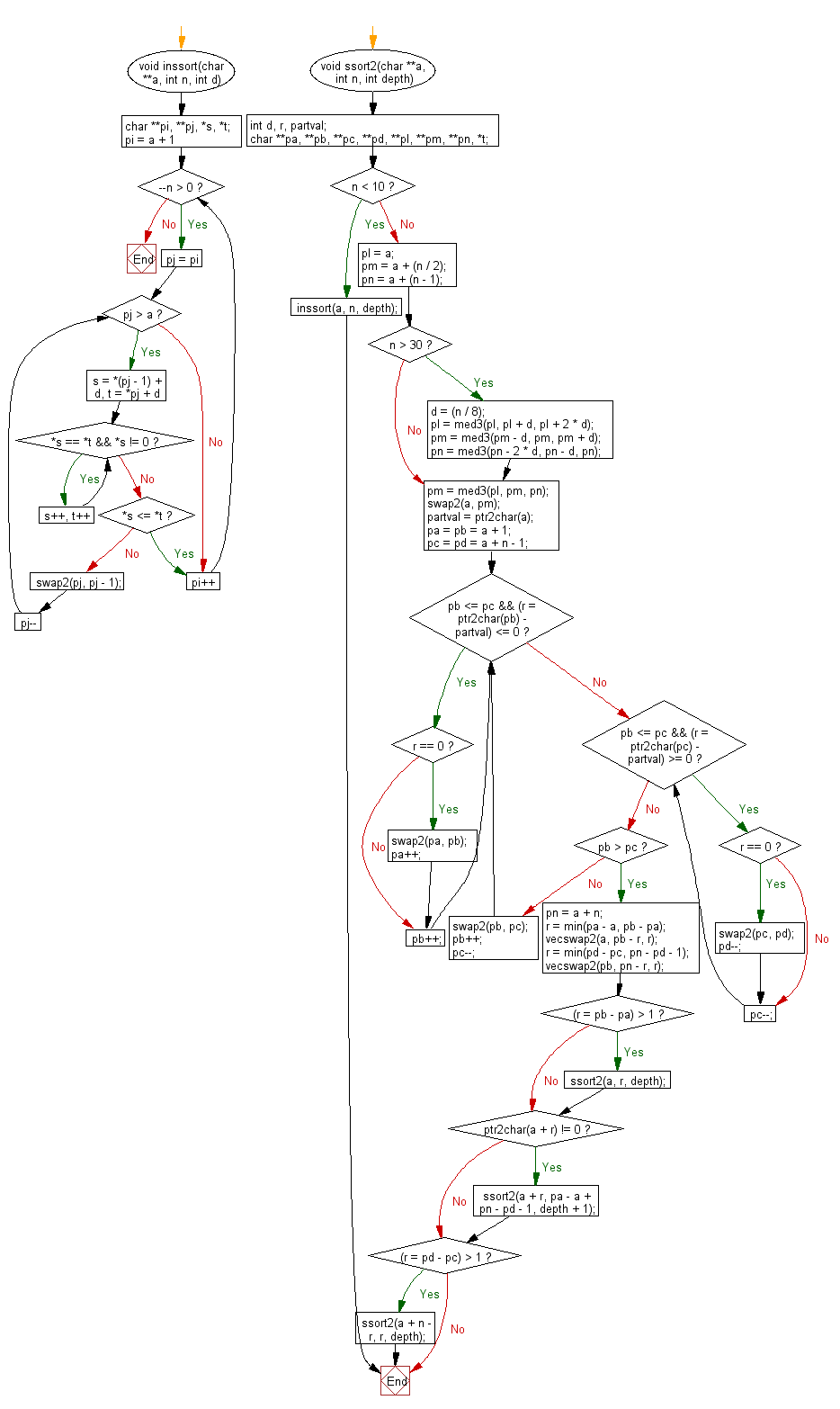
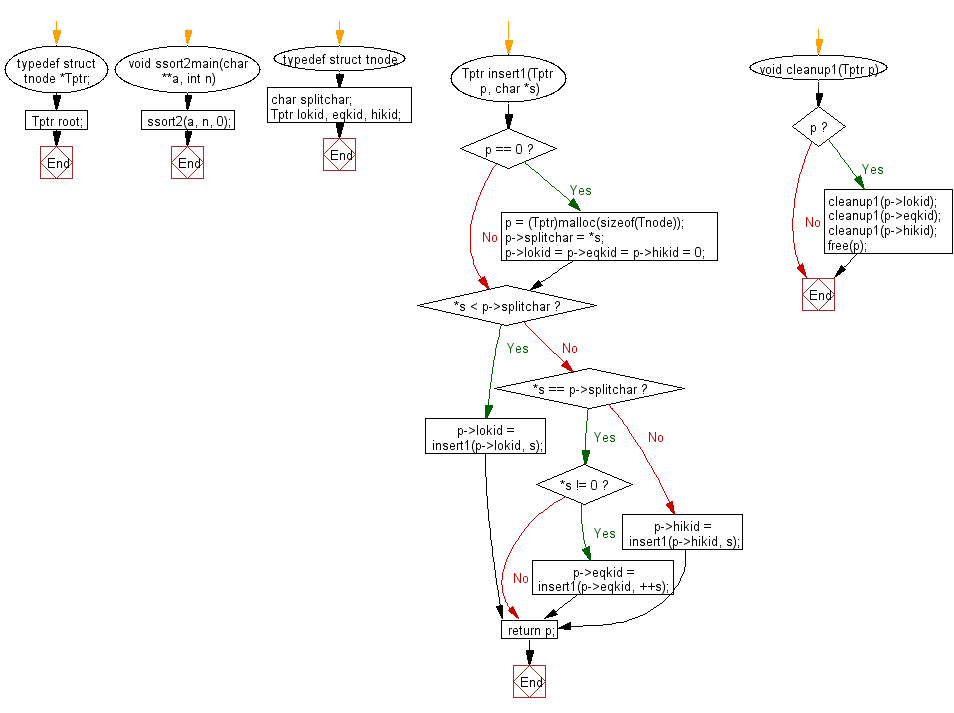
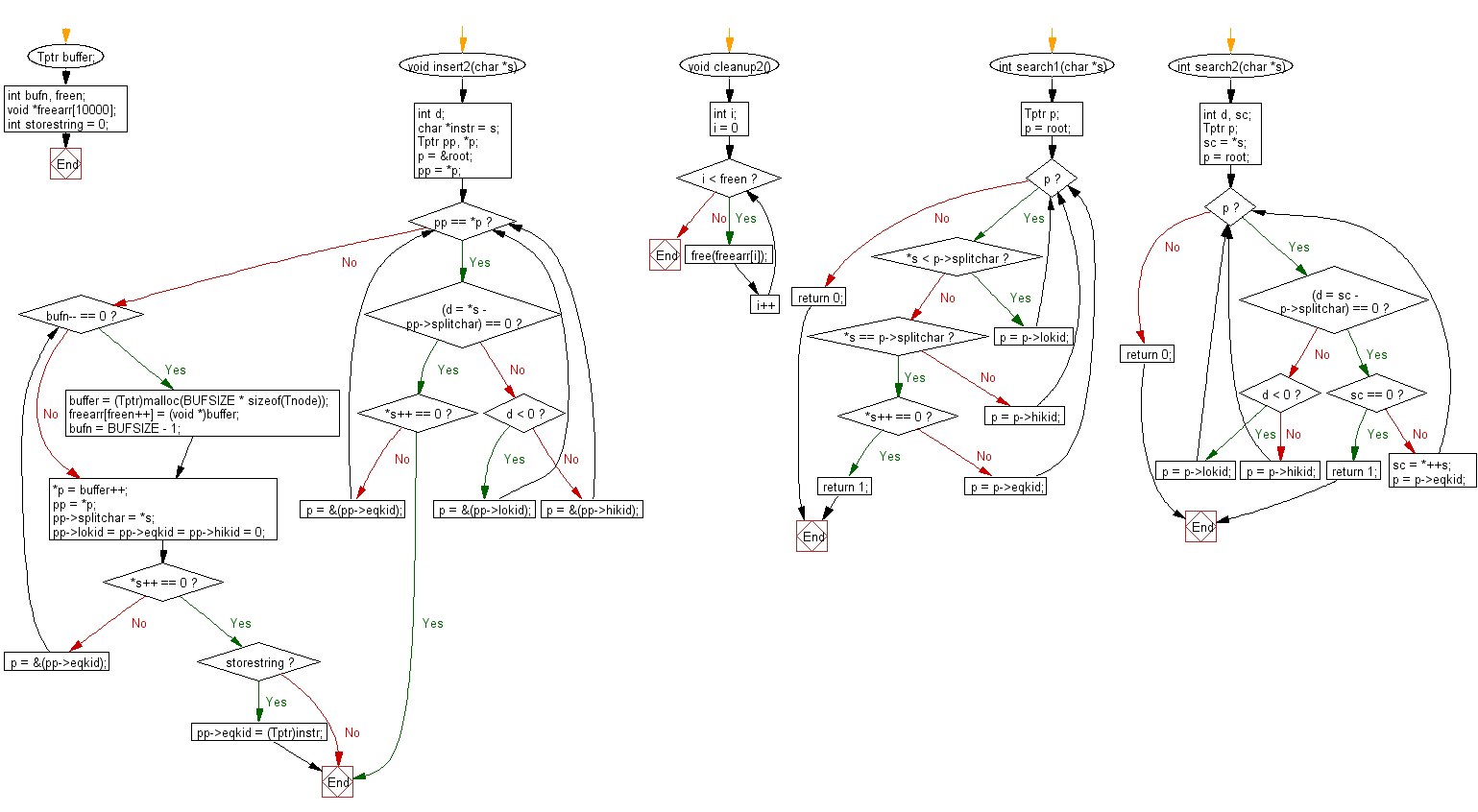
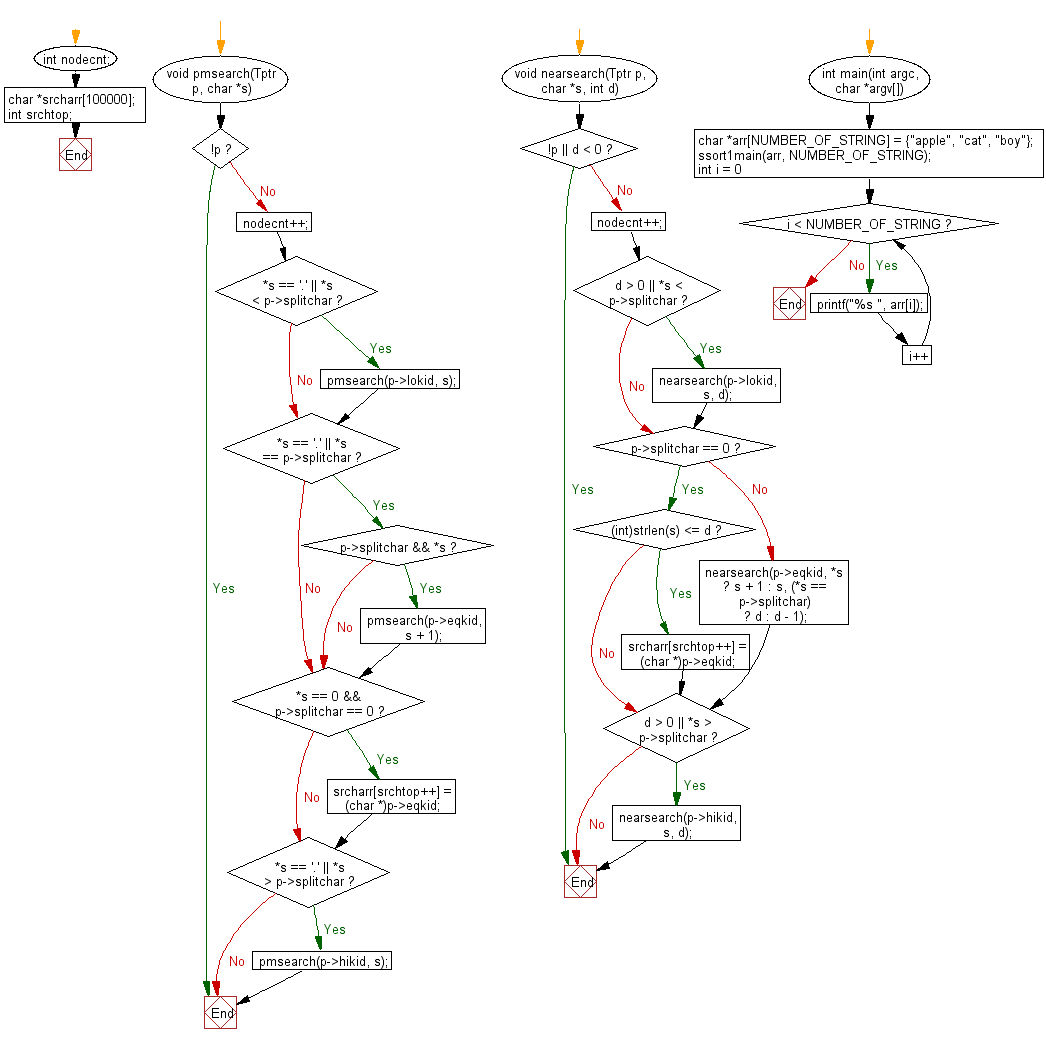
For more Practice: Solve these Related Problems:
- Write a C program to implement multi-key quicksort to sort an array of strings with common prefixes.
- Write a C program to perform three-way partitioning in multi-key quicksort for an array of strings.
- Write a C program to sort an array of structures containing strings using multi-key quicksort.
- Write a C program to implement multi-key quicksort and display the sorted array with detailed key breakdown.
Go to:
PREV : Pancake Sort Variants.
NEXT : Comb Sort Variants.
C Programming Code Editor:
Have another way to solve this solution? Contribute your code (and comments) through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
