C Exercises: Find the median of the elements in a queue
13. Queue Median Calculation
Write a C program to find the median of the elements in a queue.
From Wikipedia,
In statistics and probability theory, the median is the value separating the higher half from the lower half of a data sample, a population, or a probability distribution.
The median of a finite list of numbers is the "middle" number, when those numbers are listed in order from smallest to greatest.
If the data set has an odd number of observations, the middle one is selected. For example, the following list of seven numbers,
1, 3, 3, 6, 7, 8, 9
has the median of 6, which is the fourth value.
If the data set has an even number of observations, there is no distinct middle value and the median is usually defined to be the arithmetic mean of the two middle values. For example, this data set of 8 numbers1, 2, 3, 4, 5, 6, 8, 9 has a median value of 4.5, that is (4+5)/2 . (In more technical terms, this interprets the median as the fully trimmed mid-range).
Sample Solution:
C Code:
#include <stdio.h>
#define MAX_SIZE 100 // Define the maximum size of the queue
int queue[MAX_SIZE]; // Array to store elements of the queue
int front = -1, back = -1; // Initialize front and back pointers
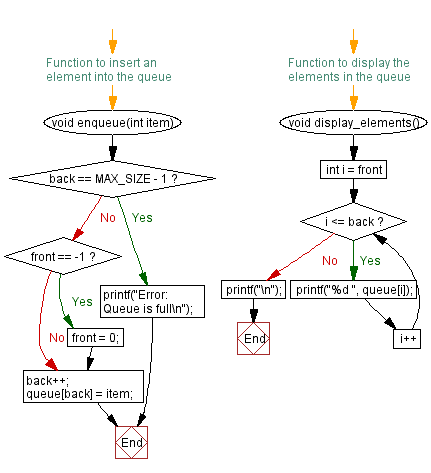
// Function to insert an element into the queue
void enqueue(int item) {
if (back == MAX_SIZE - 1) { // Check if the queue is full
printf("Error: Queue is full\n"); // Print error message if the queue is full
return;
}
if (front == -1) { // Check if the queue is empty
front = 0; // If empty, set front to 0
}
back++; // Increment the back pointer
queue[back] = item; // Add the item to the queue
}
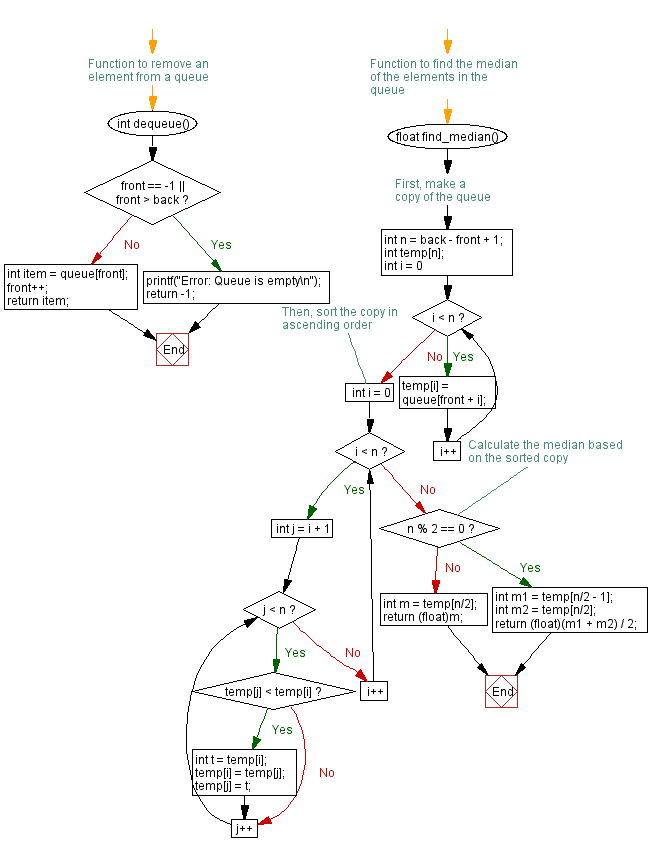
// Function to remove an element from a queue
int dequeue() {
if (front == -1 || front > back) { // Check if the queue is empty
printf("Error: Queue is empty\n"); // Print error message if the queue is empty
return -1; // Return -1 to indicate an empty queue
}
int item = queue[front]; // Get the front element of the queue
front++; // Move the front pointer to the next element
return item; // Return the removed element
}
// Function to find the median of the elements in the queue
float find_median() {
// First, make a copy of the queue
int n = back - front + 1; // Calculate the number of elements in the queue
int temp[n]; // Create a temporary array to store the elements
for (int i = 0; i < n; i++) { // Copy elements from the queue to the temporary array
temp[i] = queue[front + i];
}
// Then, sort the copy in ascending order using bubble sort algorithm
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (temp[j] < temp[i]) { // Swap elements if out of order
int t = temp[i];
temp[i] = temp[j];
temp[j] = t;
}
}
}
// Calculate the median based on the sorted copy
if (n % 2 == 0) { // If the number of elements is even
int m1 = temp[n/2 - 1]; // Get the two middle elements
int m2 = temp[n/2];
return (float)(m1 + m2) / 2; // Calculate and return the average of the two middle elements
} else { // If the number of elements is odd
int m = temp[n/2]; // Get the middle element
return (float)m; // Return the middle element as the median
}
}
// Function to display the elements in the queue
void display_elements() {
for (int i = front; i <= back; i++) { // Loop through the elements of the queue
printf("%d ", queue[i]); // Print the current element
}
printf("\n"); // Print a newline after displaying all elements
}
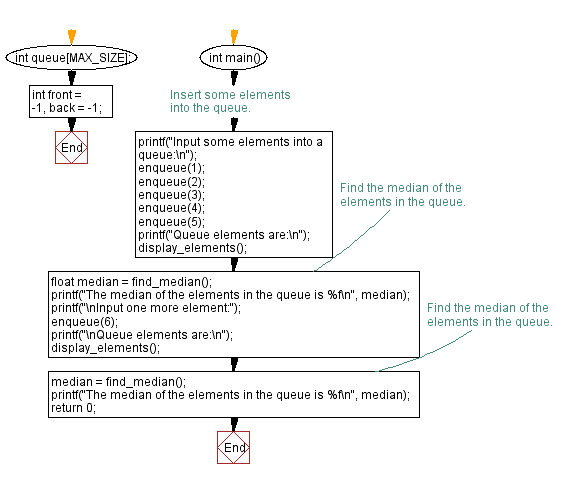
int main() {
// Insert some elements into the queue.
printf("Input some elements into a queue:\n");
enqueue(1);
enqueue(2);
enqueue(3);
enqueue(4);
enqueue(5);
printf("Queue elements are:\n");
display_elements();
// Find the median of the elements in the queue.
float median = find_median();
printf("The median of the elements in the queue is %f\n", median);
printf("\nInput one more element:");
enqueue(6);
printf("\nQueue elements are:\n");
display_elements();
// Find the median of the elements in the queue.
median = find_median();
printf("The median of the elements in the queue is %f\n", median);
return 0;
}
Output:
Input some elements into a queue: Queue elements are: 1 2 3 4 5 The median of the elements in the queue is 3.000000 Input one more element: Queue elements are: 1 2 3 4 5 6 The median of the elements in the queue is 3.500000
Flowchart
For more Practice: Solve these Related Problems:
- Write a C program to dynamically calculate the median of a queue as elements are enqueued and dequeued.
- Write a C program to compute the median of a linked list queue using a two-pointer technique.
- Write a C program to find the median in a circular queue after each dequeue operation with minimal recomputation.
- Write a C program to maintain a sorted auxiliary structure for a queue to retrieve the median in constant time.
C Programming Code Editor:
Have another way to solve this solution? Contribute your code (and comments) through Disqus.
Previous: Sort a queue in ascending order.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.