C Exercises: Check whether a given number with base b is a Niven number or not

Last update on August 05 2025 12:55:58 (UTC/GMT +8 hours)

38. Niven Number Check (Base b) Variants

Write a C program to check whether a given number with base b (2 <= b<= 10) is a Niven number or not.
From Wikipedia,
In recreational mathematics, a harshad number (or Niven number) in a given number base, is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers in base n are also known as n-harshad (or n-Niven) numbers. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "harshad" comes from the Sanskrit harṣa (joy) + da (give), meaning joy-giver. The term “Niven number” arose from a paper delivered by Ivan M. Niven at a conference on number theory in 1977. All integers between zero and n are n-harshad numbers.
The number 18 is a harshad number in base 10, because the sum of the digits 1 and 8 is 9 (1 + 8 = 9), and 18 is divisible by 9 (since 18/9 = 2, and 2 is a whole number).

Test Data
Input: base 10: Number 3
Output: 3 is a Niven Number
Input: base 10: Number 18
Output: 18 is a Niven Number
Input: base 10: Number 15
Output: 15 is not a Niven Number

Sample Solution:

C Code:

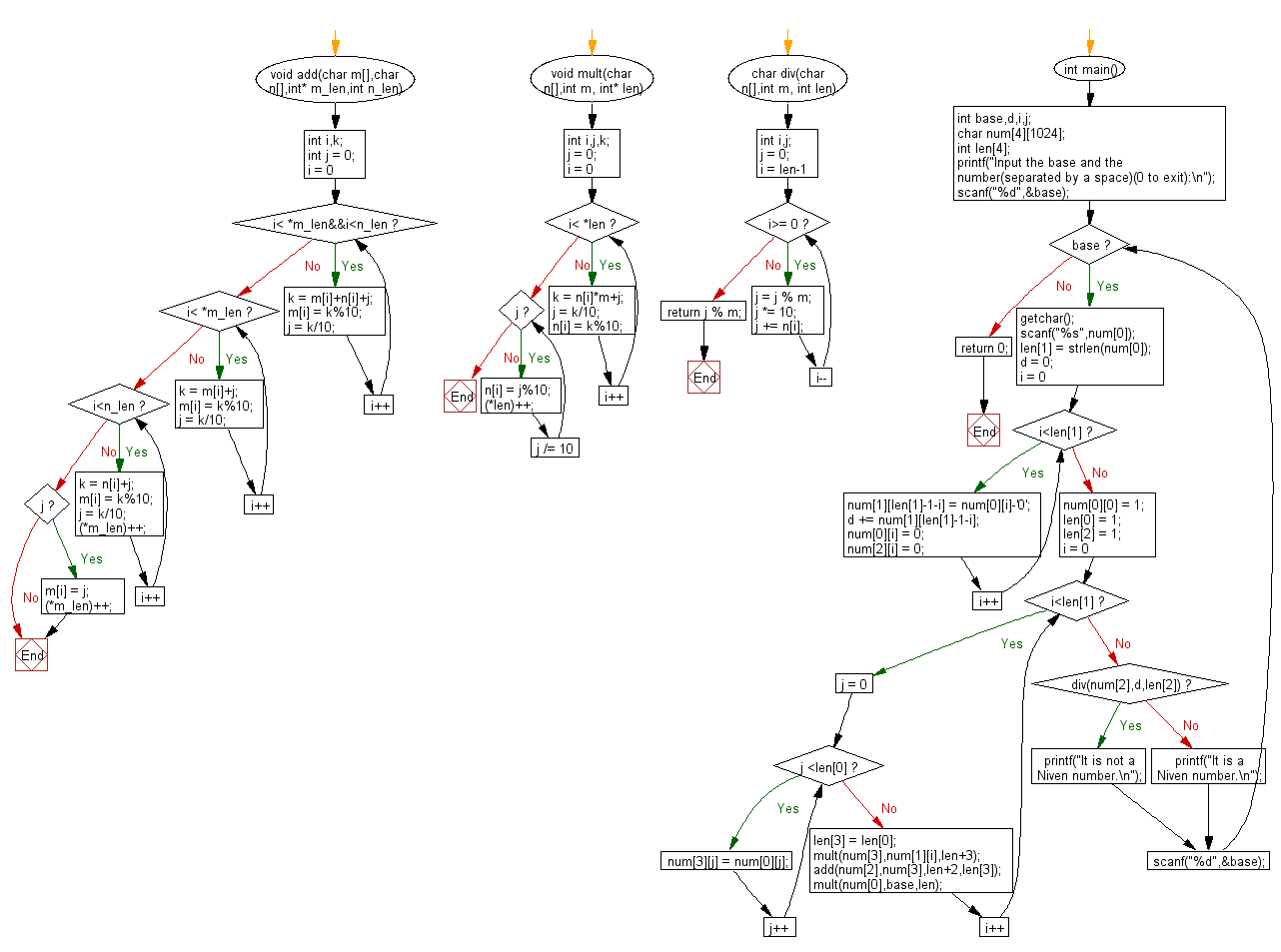
#include <stdio.h>
#include <string.h>

// Function to perform addition of two numbers represented as arrays
void add(char m[], char n[], int* m_len, int n_len) {
    int i, k;
    int j = 0;

    // Addition of digits until the length of the shorter number
    for (i = 0; i < *m_len && i < n_len; i++) {
        k = m[i] + n[i] + j;
        m[i] = k % 10;
        j = k / 10;
    }

    // Continue addition for the remaining digits of the longer number
    for (; i < *m_len; i++) {
        k = m[i] + j;
        m[i] = k % 10;
        j = k / 10;
    }

    // If there's a carry after addition, update the length and carry the digit
    for (; i < n_len; i++) {
        k = n[i] + j;
        m[i] = k % 10;
        j = k / 10;
        (*m_len)++;
    }

    // If there's still a carry after all additions, add the carry as a new digit
    if (j) {
        m[i] = j;
        (*m_len)++;
    }
}

// Function to perform multiplication of a number represented as an array by an integer
void mult(char n[], int m, int* len) {
    int i, j, k;
    j = 0;

    // Multiply each digit of the number by 'm'
    for (i = 0; i < *len; i++) {
        k = n[i] * m + j;
        j = k / 10;
        n[i] = k % 10;
    }

    // If there's a carry after multiplication, extend the number length with the carry
    for (; j; j /= 10) {
        n[i] = j % 10;
        (*len)++;
        i++;
    }
}

// Function to perform division of a number represented as an array by an integer
char div(char n[], int m, int len) {
    int i, j;
    j = 0;

    // Perform division by taking each digit and calculating the remainder
    for (i = len - 1; i >= 0; i--) {
        j = j % m;
        j *= 10;
        j += n[i];
    }
    return j % m;
}

// Main function
int main() {
    int base, d, i, j;
    char num[4][1024];
    int len[4];

    // Input base and number, perform Niven number check
    printf("Input the base and the number (separated by a space) (0 to exit):\n");
    scanf("%d", &base);

    // Continue until base is not 0
    while (base) {
        getchar();
        scanf("%s", num[0]);
        len[1] = strlen(num[0]);
        d = 0;

        // Reverse the input number and calculate its digit sum
        for (i = 0; i < len[1]; i++) {
            num[1][len[1] - 1 - i] = num[0][i] - '0';
            d += num[1][len[1] - 1 - i];
            num[0][i] = 0;
            num[2][i] = 0;
        }
        num[0][0] = 1;
        len[0] = 1;
        len[2] = 1;

        // Calculate the Niven number
        for (i = 0; i < len[1]; i++) {
            for (j = 0; j < len[0]; j++) {
                num[3][j] = num[0][j];
            }
            len[3] = len[0];
            mult(num[3], num[1][i], len + 3);
            add(num[2], num[3], len + 2, len[3]);
            mult(num[0], base, len);
        }

        // Check if it's a Niven number or not and display the result
        if (div(num[2], d, len[2])) {
            printf("It is not a Niven number.\n");
        } else {
            printf("It is a Niven number.\n");
        }

        // Input the base again to continue or exit
        scanf("%d", &base);
    }

    return 0;
}

Sample Output:

 Input the base and the number(separated by a space)(0 to exit): 10 3 0
It is a Niven number.

Flowchart:

For more Practice: Solve these Related Problems:

Write a C program to check if a number in a given base is a Niven number by summing its digits.
Write a C program to verify Niven numbers across multiple bases and compare their properties.
Write a C program to list Niven numbers for a specified base and display the digit sum division process.
Write a C program to optimize Niven number checking by efficiently converting numbers to the given base.

Go to:

PREV : Keith Number Check with Explanation Variants.
NEXT : C String Exercises Home

C Programming Code Editor:

Contribute your code and comments through Disqus.