Prim's Algorithm for minimum Spanning Tree in C
8. Prim's Algorithm Extended Challenges
Write a C program that implements Prim's algorithm to find the minimum spanning tree of a connected, undirected graph in C.
From Wikipedia,
In computer science, Prim's algorithm (also known as Jarník's algorithm) is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.
Following Prim's algorithm starting at vertex A. In the third step, edges BD and AB both have weight 2, so BD is chosen arbitrarily. After that step, AB is no longer a candidate for addition to the tree because it links two nodes that are already in the tree.
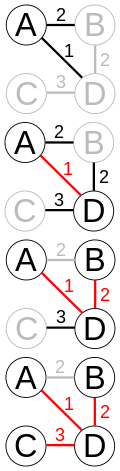
Source: Wikipdeia
Sample Solution:
C Code:
#include <stdio.h>
#include <limits.h>
#define MAX_VERTICES 100
// Function to find the vertex with the minimum key value
int minKey(int key[], int mstSet[], int vertices) {
int min = INT_MAX, minIndex;
for (int v = 0; v < vertices; v++) {
if (!mstSet[v] && key[v] < min) {
min = key[v];
minIndex = v;
}
}
return minIndex;
}
// Function to print the constructed MST stored in parent[]
void printMST(int parent[], int graph[MAX_VERTICES][MAX_VERTICES], int vertices) {
printf("Edge \tWeight\n");
for (int i = 1; i < vertices; i++) {
printf("%d - %d \t%d\n", parent[i], i, graph[i][parent[i]]);
}
}
// Function to implement Prim's algorithm for a given graph
void primMST(int graph[MAX_VERTICES][MAX_VERTICES], int vertices) {
int parent[MAX_VERTICES]; // Array to store the constructed MST
int key[MAX_VERTICES]; // Key values used to pick the minimum weight edge
int mstSet[MAX_VERTICES]; // To represent set of vertices included in MST
// Initialize all keys as INFINITE and mstSet[] as false
for (int i = 0; i < vertices; i++) {
key[i] = INT_MAX;
mstSet[i] = 0;
}
// Always include the first vertex in the MST
key[0] = 0; // Make key 0 so that this vertex is picked as the first vertex
parent[0] = -1; // First node is always the root of the MST
// The MST will have vertices-1 edges
for (int count = 0; count < vertices - 1; count++) {
// Pick the minimum key vertex from the set of vertices not yet included in the MST
int u = minKey(key, mstSet, vertices);
// Add the picked vertex to the MST Set
mstSet[u] = 1;
// Update key value and parent index of the adjacent vertices
for (int v = 0; v < vertices; v++) {
// graph[u][v] is non-zero only for adjacent vertices of m
// mstSet[v] is false for vertices not yet included in MST
// Update the key only if the graph[u][v] is smaller than the key[v]
if (graph[u][v] && !mstSet[v] && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
// Print the constructed MST
printMST(parent, graph, vertices);
}
int main() {
int vertices;
// Input the number of vertices
printf("Input the number of vertices: ");
scanf("%d", &vertices);
if (vertices <= 0 || vertices > MAX_VERTICES) {
printf("Invalid number of vertices. Exiting...\n");
return 1;
}
int graph[MAX_VERTICES][MAX_VERTICES];
// Input the adjacency matrix representing the graph
printf("Input the adjacency matrix for the graph:\n");
for (int i = 0; i < vertices; i++) {
for (int j = 0; j < vertices; j++) {
scanf("%d", &graph[i][j]);
}
}
// Perform Prim's algorithm to find the MST
primMST(graph, vertices);
return 0;
}
Output:
Input the number of vertices: 5 Input the adjacency matrix for the graph: 0 2 0 6 0 2 0 3 8 5 0 3 0 0 7 6 8 0 0 9 0 5 7 9 0 Edge Weight 0 - 1 2 1 - 2 3 0 - 3 6 1 - 4 5
Explanation:
In the exercise above,
- minKey function: Finds the vertex with the minimum key value in the 'key' array, considering only the vertices not yet included in the Minimum Spanning Tree (MST).
- printMST function: Prints the edges and weights of the constructed MST, using the parent array.
- primMST function: Implements Prim's algorithm. It initializes key values, sets, and 'parent' array. It iteratively selects the vertex with the minimum key value from the set of vertices not included in MST, updates key values and parent indices of adjacent vertices.
- The program takes user input for the number of vertices and the adjacency matrix representing the graph.
- The output is the edges and their weights in the MST.
Flowchart:
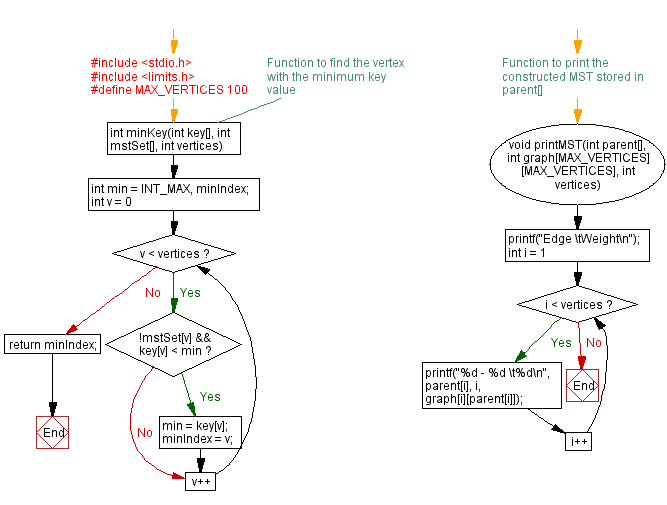
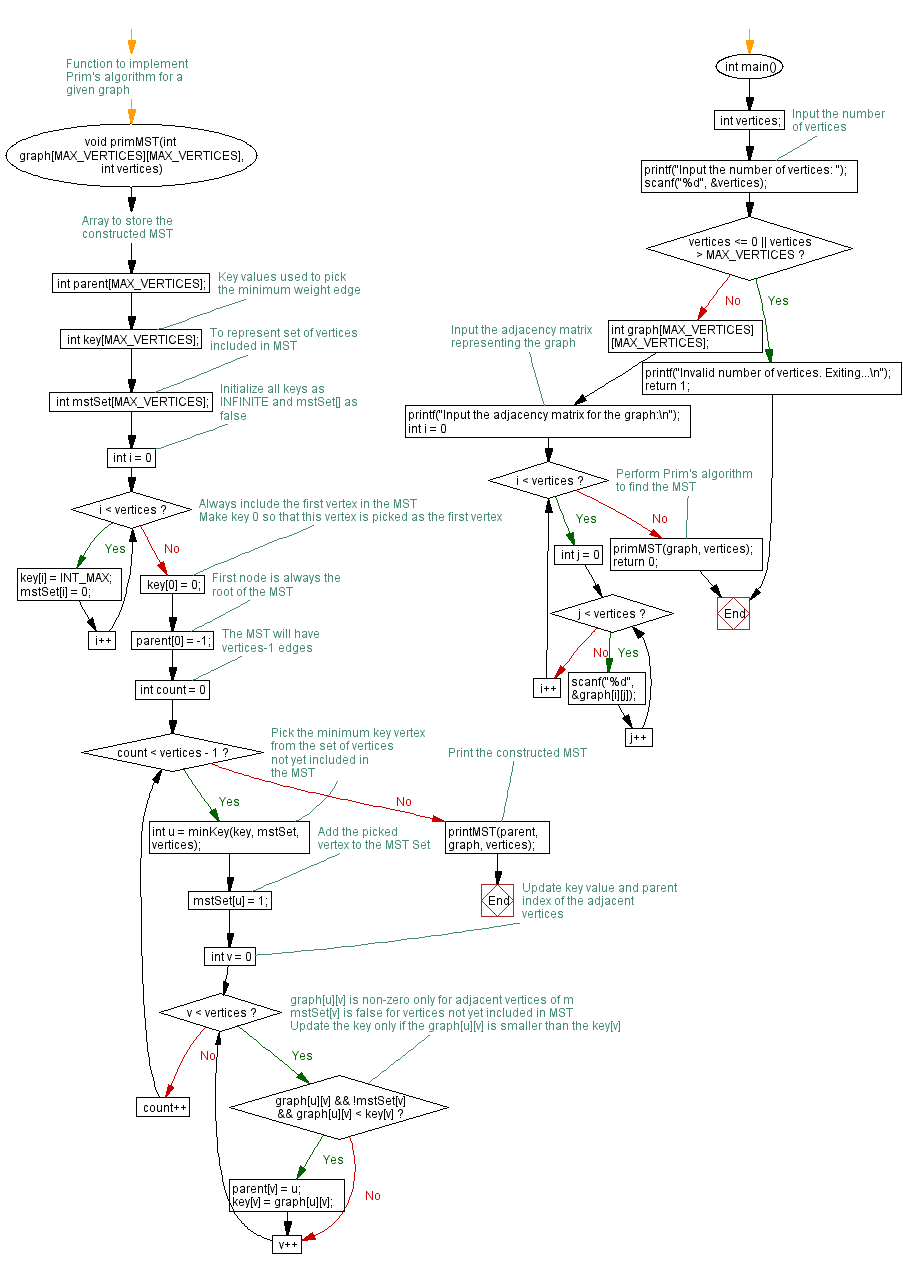
For more Practice: Solve these Related Problems:
- Write a C program to implement Prim's algorithm on a weighted graph using an adjacency matrix and print the MST edges.
- Write a C program to optimize Prim's algorithm using a min-heap and compare its performance with the basic approach.
- Write a C program to run Prim's algorithm on a graph with potential negative weights and handle invalid cases gracefully.
- Write a C program to implement a modified Prim's algorithm that displays the intermediate MST at each iteration.
Go to:
PREV : Topological Sorting Extended Challenges.
NEXT : Dijkstra's Algorithm Extended Challenges.
C Programming Code Editor:
Have another way to solve this solution? Contribute your code (and comments) through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
