Cycle detection in Graph: C Program implementation

Last update on December 20 2024 13:05:13 (UTC/GMT +8 hours)

Write a C program that implements a function in C to check whether a given graph contains a cycle or not.

From Wikipedia,

In graph theory, a cycle in a graph is a non-empty trail in which only the first and last vertices are equal. A directed cycle in a directed graph is a non-empty directed trail in which only the first and last vertices are equal.

A graph without cycles is called an acyclic graph. A directed graph without directed cycles is called a directed acyclic graph. A connected graph without cycles is called a tree.

Here is a graph with edges colored to illustrate a closed walk, H–A–B–A–H, in green; a circuit which is a closed walk in which all edges are distinct, B–D–E–F–D–C–B, in blue; and a cycle which is a closed walk in which all vertices are distinct, H–D–G–H, in red.

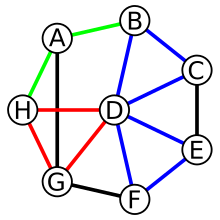
Source: Wikipedia

Sample Solution:

C Code:

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTICES 100

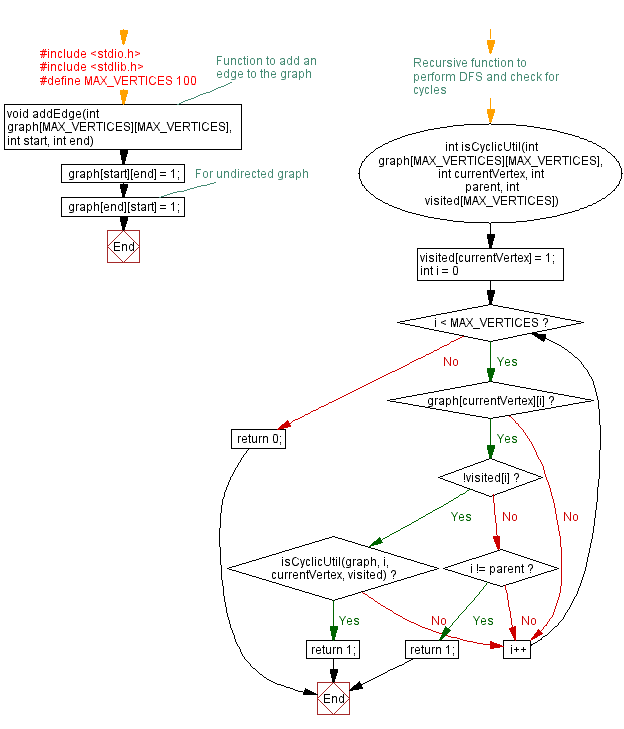
// Function to add an edge to the graph
void addEdge(int graph[MAX_VERTICES][MAX_VERTICES], int start, int end) {
    graph[start][end] = 1;
    graph[end][start] = 1; // For undirected graph
}

// Recursive function to perform DFS and check for cycles
int isCyclicUtil(int graph[MAX_VERTICES][MAX_VERTICES], int currentVertex, int parent, int visited[MAX_VERTICES]) {
    visited[currentVertex] = 1;

    for (int i = 0; i < MAX_VERTICES; i++) {
        if (graph[currentVertex][i]) {
            if (!visited[i]) {
                if (isCyclicUtil(graph, i, currentVertex, visited))
                    return 1;
            } else if (i != parent) {
                return 1;
            }
        }
    }

    return 0;
}

// Function to check whether a graph contains a cycle
int isCyclic(int graph[MAX_VERTICES][MAX_VERTICES], int vertices) {
    int visited[MAX_VERTICES] = {0};

    for (int i = 0; i < vertices; i++) {
        if (!visited[i]) {
            if (isCyclicUtil(graph, i, -1, visited))
                return 1;
        }
    }

    return 0;
}

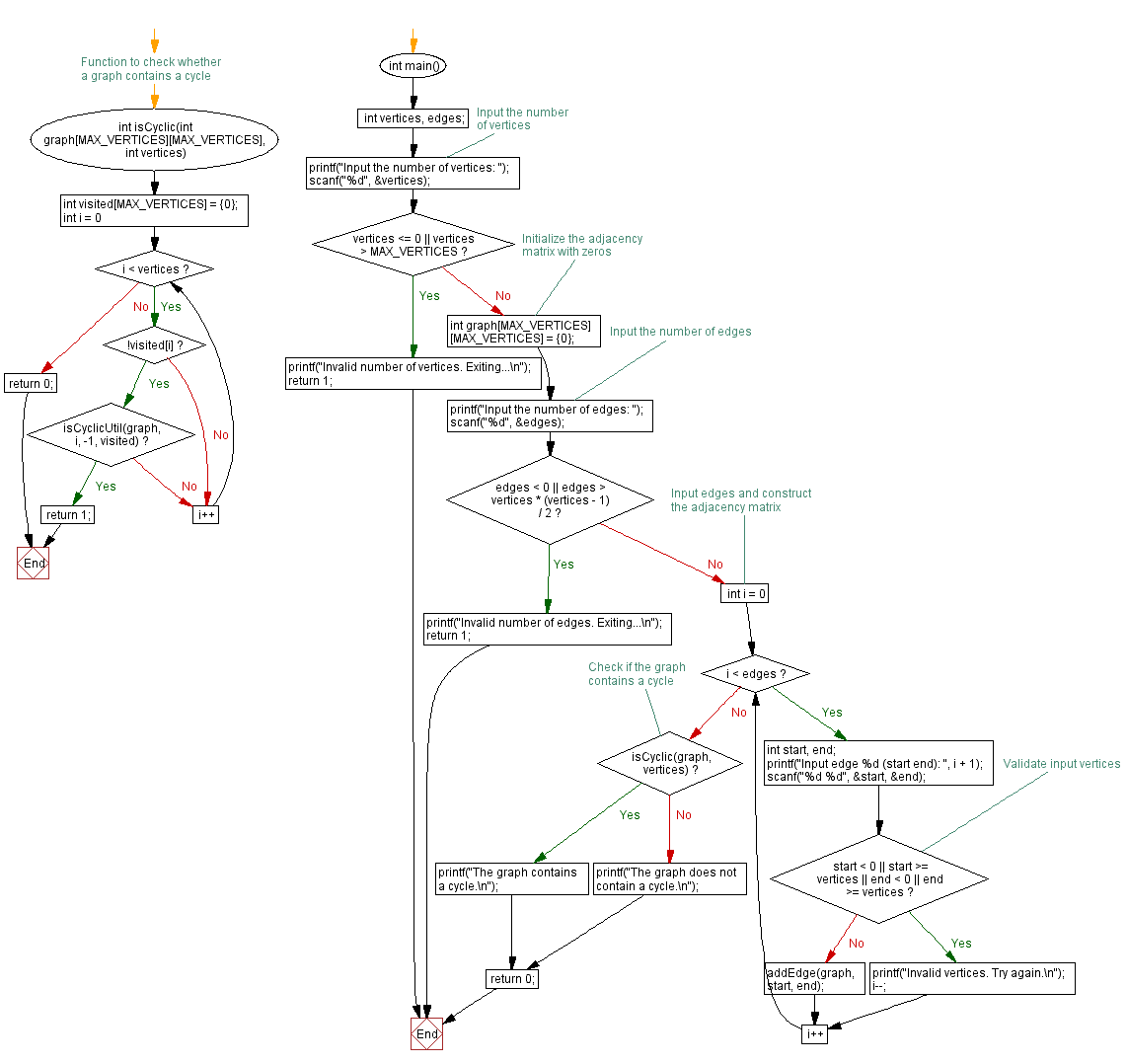
int main() {
    int vertices, edges;

    // Input the number of vertices
    printf("Input the number of vertices: ");
    scanf("%d", &vertices);

    if (vertices <= 0 || vertices > MAX_VERTICES) {
        printf("Invalid number of vertices. Exiting...\n");
        return 1;
    }

    int graph[MAX_VERTICES][MAX_VERTICES] = {0}; // Initialize the adjacency matrix with zeros

    // Input the number of edges
    printf("Input the number of edges: ");
    scanf("%d", &edges);

    if (edges < 0 || edges > vertices * (vertices - 1) / 2) {
        printf("Invalid number of edges. Exiting...\n");
        return 1;
    }

    // Input edges and construct the adjacency matrix
    for (int i = 0; i < edges; i++) {
        int start, end;
        printf("Input edge %d (start end): ", i + 1);
        scanf("%d %d", &start, &end);

        // Validate input vertices
        if (start < 0 || start >= vertices || end < 0 || end >= vertices) {
            printf("Invalid vertices. Try again.\n");
            i--;
            continue;
        }

        addEdge(graph, start, end);
    }

    // Check if the graph contains a cycle
    if (isCyclic(graph, vertices))
        printf("The graph contains a cycle.\n");
    else
        printf("The graph does not contain a cycle.\n");

    return 0;
}

Output:

Input the number of vertices: 4
Input the number of edges: 4
Input edge 1 (start end): 0 1
Input edge 2 (start end): 1 2
Input edge 3 (start end): 2 3
Input edge 4 (start end): 3 0
The graph contains a cycle.
Note: Here we have a simple cycle with four vertices: 0 → 1 → 2 → 3 → 0.

Explanation:

In the exercise above,

• addEdge Function:
• Adds an undirected edge between two vertices in the graph.
• isCyclicUtil Function:
• Recursive function that performs DFS traversal and checks for cycles.
• It maintains an array 'visited' to mark visited vertices.
• If a vertex i is not visited, it recursively calls the function for i.
• If a vertex i is visited and is not the parent of the current vertex, then there is a cycle.
• isCyclic Function:
• Initiates DFS traversal for each unvisited vertex.
• Calls "isCyclicUtil()" for each unvisited vertex.
• If "isCyclicUtil()" returns true for any vertex, it means a cycle is present in the graph.
• Main Function:
• Takes input for the number of vertices and edges in the graph.
• Constructs the adjacency matrix for the graph by taking input for each edge.
• Calls "isCyclic()" function to check for the presence of a cycle.
• Prints whether the graph contains a cycle or not.

Flowchart:

C Programming Code Editor:

Click to Open Editor

Previous: Breadth-First Search (BFS) Traversal in Graph: C Program Example.
Next: Topological sorting of directed Acyclic Graph (DAG) in C.