C Exercises: Check whether a given number is an armstrong number or not
29. Armstrong Number Check
Write a C program to check whether a given number is an Armstrong number or not.
An Armstrong number (also known as a Narcissistic number) for a given number of digits is a number that is equal to the sum of its own digits each raised to the power of the number of digits. For example, 153 is an Armstrong number because 153 = 13+53+33. 1634 is an Armstrong number because 1634 = 14+64+34+44 = 1 + 1296 + 81 + 256
Uses and Applications of Armstrong Numbers
- Mathematical Curiosity and Education:
- Educational Tool: Armstrong numbers illustrate properties of numbers and digit manipulation.
- Algorithm Design: Used in computer science to teach loops, conditionals, and mathematical operations.
- Programming Challenges:
- Algorithm Efficiency: Common in coding exercises to improve algorithm design and optimization skills.
- Cryptography:
- Hash Functions: Basis for simple hash functions through digit manipulation and summation.
- Puzzle creation:
- Math Puzzles: Used in brainteasers to develop logical thinking and problem-solving skills.
Educational Example Topics
- Understanding Powers: Learning how to raise numbers to specific powers and sum them.
- Modular Arithmetic: Extracting digits using modulus and division operations.
- Loop Constructs: Using loops to iterate through digits of a number.
- Conditional Statements: Using if-else conditions to check numeric properties.
Test Data :
Input a number: 153
Expected Output :
153 is an Armstrong number.
Sample Solution:
C Code:
#include <stdio.h>
#include <math.h> // Include the math library for the pow function
int main() {
int num, temp, originalNum, remainder, sum = 0, n = 0; // Declare variables
// Prompt the user to input a number
printf("Input a number: ");
scanf("%d", &num);
originalNum = num;
// Calculate the number of digits in the input number
for (temp = num; temp != 0; n++) {
temp /= 10;
}
// Calculate the sum of the nth powers of each digit
for (temp = num; temp != 0; temp /= 10) {
remainder = temp % 10;
sum += pow(remainder, n);
}
// Check if the sum is equal to the original number
if (sum == originalNum) {
printf("%d is an Armstrong number.\n", originalNum);
} else {
printf("%d is not an Armstrong number.\n", originalNum);
}
return 0;
}
Output:
Input a number: 153 153 is an Armstrong number.
Input a number: 1634 1634 is an Armstrong number.
Explanation:
- Include Libraries: The stdio.h library is used for input and output functions, and the math.h library is included for the "pow()" function, which calculates the power of a number.
- Declare Variables: Variables are declared for storing the input number (num), a copy of the original number (originalNum), the remainder of the division (remainder), the sum of the powers of the digits (sum), and the number of digits in the number (n).
- Input the Number: The user inputs a number, which is read and stored in the num variable.
- Calculate the Number of Digits: A loop is used to determine the number of digits in the input number. The variable temp is used to temporarily store the number while it is divided by 10 in each iteration until it becomes 0. The number of iterations (n) gives the number of digits.
- Sum the Powers of the Digits: Another loop extracts each digit from the number, raises it to the power of n, and adds the result to sum.
- Check and Output the Result: The program checks if the sum of the nth powers of the digits is equal to the original number. If true, it prints that the number is an Armstrong number; otherwise, it prints that it is not.
Flowchart:
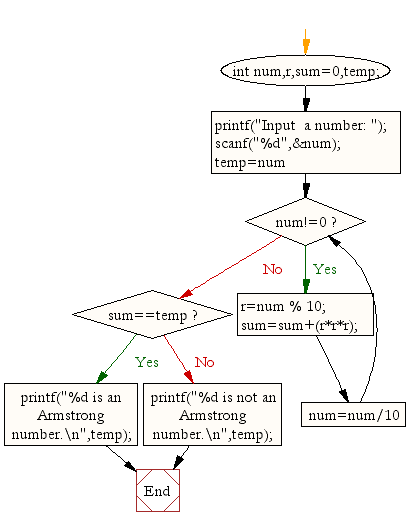
Armstrong number: Function-based Solution
SQL Code:
#include <stdio.h> // Include the standard input/output header file
#include <math.h> // Include the math header file for the pow function
// Function prototype for isArmstrong, which checks if a number is an Armstrong number
int isArmstrong(int num);
int main() {
int num; // Declare a variable to hold the input number
char choice; // Declare a variable to hold the user's choice to continue or not
do {
printf("Input a number: "); // Prompt the user to input a number
scanf("%d", &num); // Read the input number from the user
// Check if the number is an Armstrong number and print the result
if (isArmstrong(num)) {
printf("%d is an Armstrong number.\n", num);
} else {
printf("%d is not an Armstrong number.\n", num);
}
// Ask the user if they want to check another number
printf("Do you want to check another number? (y/n): ");
scanf(" %c", &choice); // Read the user's choice
} while (choice == 'y' || choice == 'Y'); // Repeat the process if the user enters 'y' or 'Y'
}
// Function to check if a number is an Armstrong number
int isArmstrong(int num) {
int originalNum, remainder, sum = 0, n = 0, temp;
originalNum = num; // Store the original number
temp = num; // Copy the number to a temporary variable
// Count the number of digits in the number
while (temp != 0) {
temp /= 10; // Remove the last digit
n++; // Increment the digit count
}
temp = num; // Reset the temporary variable to the original number
// Calculate the sum of the nth powers of the digits
while (temp != 0) {
remainder = temp % 10; // Get the last digit
sum += pow(remainder, n); // Add the nth power of the digit to the sum
temp /= 10; // Remove the last digit
}
return (sum == originalNum); // Return true if the sum equals the original number
}
Output:
Input a number: 151 151 is not an Armstrong number. Do you want to check another number? (y/n): y Input a number: 153 153 is an Armstrong number. Do you want to check another number? (y/n): y Input a number: 1634 1634 is an Armstrong number. Do you want to check another number? (y/n): n
Explanation:
- The above code includes the necessary headers for input/output operations and mathematical functions.
- The main function handles user interaction, asking for input numbers and checking if they are Armstrong numbers using the isArmstrong function.
- The isArmstrong function checks if the given number is an Armstrong number by:
- Count the number of digits in the number.
- Calculating the sum of the digits each raised to the power of the total number of digits.
- Comparing the calculated sum to the original number and returning whether they are equal.
Frequently Asked Questions (FAQ) on Armstrong number
1. What is an Armstrong number?
An Armstrong number, also known as a narcissistic number, is a number that is equal to the sum of its own digits each raised to the power of the number of digits.
2. Why are Armstrong numbers important?
Armstrong numbers are often used in computer science and mathematics for teaching purposes, demonstrating properties of numbers and algorithms related to number theory and digital operations.
3. How are Armstrong numbers used in programming?
Armstrong numbers are used in programming challenges to help students and developers practice loops, conditionals, and mathematical computations. They also serve as good examples for learning about functions and modular programming.
4. What are the applications of Armstrong numbers?
Beyond educational purposes, Armstrong numbers have limited practical applications but are useful in cryptographic algorithms, hashing functions, and other areas where unique numerical properties are beneficial.
5. How can Armstrong numbers be verified?
Verification typically involves summing the digits of a number, each raised to the power of the number of digits, and checking if the result matches the original number. This can be done programmatically using loops or recursion.
6. Are there any known patterns or distributions for Armstrong numbers?
Armstrong numbers are relatively rare and do not follow a simple pattern. They are sparse and become less frequent as numbers grow larger, making them an interesting subject for number theory research.
7. What is the historical significance of Armstrong numbers?
Armstrong numbers were first studied in the early 20th century. Their unique properties have intrigued mathematicians and educators, leading to their inclusion in various mathematical puzzles and programming exercises.
For more Practice: Solve these Related Problems:
- Write a C program to check if a number is Armstrong using recursion to compute digit powers.
- Write a C program to verify an Armstrong number by converting the number to a string and processing each digit.
- Write a C program to check if a number is Armstrong without using loops by employing recursion only.
- Write a C program to check if a number is Armstrong and then display the sum of its digits raised to the power of the number of digits.
Go to:
PREV : Find Perfect Numbers in a Range.
NEXT : Armstrong Numbers in a Range.
C Programming Code Editor:
Have another way to solve this solution? Contribute your code (and comments) through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
